Bài 21: Bài toán về vị trí tương đối giữa mặt cầu và mặt phẳng

I. Lý thuyết 
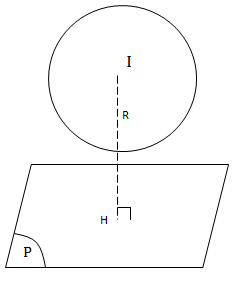
Cho mặt phẳng (P) và mặt cầu (S) có tâm I, bán kính R
TH1:
 \((S)\cap (P)=\phi\)
\(\Leftrightarrow d(I;(P))>R\)

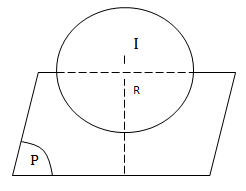
TH2: 
(P) tiếp xúc mặt cầu
\(\Leftrightarrow d(I;(P))=R\)

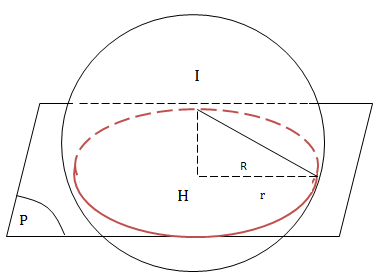
TH3: 
(P) cắt mặt cầu theo giao tuyến là đường tròn
\(\Leftrightarrow d(I;(P))<R\)
Khi đó đường tròn giao tuyến 
+ Có tâm H là hình chiếu I trên (P)
+ \(r=\sqrt{R^2-IH^2}\)
\(IH=d(I;(P))\)

II. Bài tập
VD1: Cho mặt cầu (S) \((x-1)^2+(y+1)^2+z^2=4\) và mặt phẳng \((P): x-y+2z-2=0\)
a) CMR: (P) cắt (S) theo giao tuyến là đường tròn
b) Xác định tâm, bán kính, diện tích đường tròn đó.
Giải
(S) có tâm \(I(1;-1;0), BK \ \ R=2\)
\(d(I;(P))=\frac{\left | 1+1+2.0-2 \right |}{\sqrt{1^2+(-1)^2+2^2}}=0< R\)
Vậy (P) cắt (S) theo giao tuyến là 1 đường tròn.
b)
Tâm đường tròn là hình chiếu của I trên (P) mà \(I\in (P)\) nên tâm đường tròn là I(1;-1;0)
\(bk \ r=\sqrt{R^2-IH^2}=\sqrt{R^2-d^2(I;(P))}=2\)
Diện tích đường tròn giao tuyến là \(\pi r^2=4 \pi\)
VD2: Viết phương trình mặt cầu có tâm thuộc đường thẳng \((\Delta ):\frac{x}{2}=\frac{y-1}{1}=\frac{z+1}{2}\) và tiếp xúc với 2 mặt phẳng \(\begin{matrix} (Q): x+y-2z+5=0\\ (P): 2x-y+z+2=0 \end{matrix}\)
Giải
Tâm I của mặt cầu thuộc \(\Delta\) nên I(2t; 1+t;-1+2t)
(S) tiếp xúc (P), (Q) nên
\(R=d(I;(P))=d(I;(Q))\)
\(\Leftrightarrow R=\frac{\left | 2t+1+t+2-4t+5 \right |}{\sqrt{1^2+1^2+(-2^2)}}= \frac{\left | 4t-1-t-1+2t+2 \right |}{\sqrt{2^2+(-1)^2+1^2}}\)
\(\Leftrightarrow R=\frac{\left | -t+8 \right |}{\sqrt{6}}=\frac{\left | 5t \right |}{\sqrt{6}}\)
\(\Leftrightarrow \left\{\begin{matrix} \bigg \lbrack \begin{matrix} -t+8=5t\\ -t+8=-5t \end{matrix}\\ \\ R=\frac{\left | 5t \right |}{\sqrt{6}} \ \ \ \ \ \ \ \ \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \bigg \lbrack \begin{matrix} t=\frac{4}{3}\\ t=-2 \end{matrix}\\ \\ R=\frac{\left | 5t \right |}{\sqrt{6}} \ \ \ \ \ \ \ \ \end{matrix}\right.\)
TH1:
\(t=\frac{4}{3}\Rightarrow R=\frac{20}{3\sqrt{6}}, I(\frac{8}{3};\frac{7}{3};\frac{5}{3})\)
Phương trình mặt cầu
\((x-\frac{8}{3})^2+(y-\frac{7}{3})^2+(z-\frac{5}{3})^2=\frac{200}{27}\)
TH2:
\(t=-2\Rightarrow R=\frac{10}{\sqrt{6}}, \ \ I(-4;-1;-5)\)
Phương trình mặt cầu 
\((x+4)^2+(y+1)^2+(z+5)^2=\frac{50}{3}\)
Vậy:
\((x-\frac{8}{3})^2+(y-\frac{7}{3})^2+(z-\frac{5}{3})^2=\frac{200}{27}\)
\((x+4)^2+(y+1)^2+(z+5)^2=\frac{50}{3}\)

VD3: Viết phương trình mặt cầu tâm I(2;1;3) cắt (P): 2x + y - 2z + 10 = 0 theo một đường tròn có bán kính r = 4. 
Giải

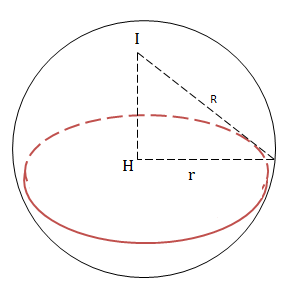
\(d=(I;(P))=\frac{\left | 2.2+1-2.3+10 \right |}{\sqrt{2^2+1^2+(-2)^2}}\)
\(=\frac{9}{3}=3\)
\(r^2=R^2-d^2(I;(P))\)
\(\Rightarrow R^2=r^2+d^2(I;(P))=4^2+3^2+5^2\Rightarrow R=5\)
Phương trình mặt cầu 
\((x-2)^2+(y-1)^2+(z-3)^2=25\)