GIỚI THIỆU BÀI HỌC
Bài học giúp học sinh biết được thế nào là tiệm cận ngang, tiệm cận đứng. Qua một số ví dụ, học sinh nắm được phương pháp tìm tiệm của đồ thị hàm số.
NỘI DUNG BÀI HỌC
A. Lý thuyết
1. Đường tiệm cận ngang
a) y = b được gọi là tiệm cận ngang của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện sau
\(\lim_{x\rightarrow -\infty } f(x) = b\)
\(\lim_{x\rightarrow +\infty } f(x) = b\)
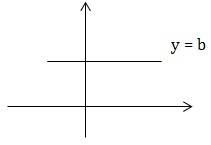
b) Chú ý
ĐK để đồ thị hàm số \(y = \frac{P(x)}{Q(x)}\) , P(x), Q(x) là các đa thức có tiệm cận ngang là bậc tử ≤ bậc mẫu.
\(y = \frac{a_nx^n + ... + a_0}{b_mx^m + ... + b_0} \ \ \ m, n \in N; a_n\neq 0; b_m\neq 0\)
ĐK có tiệm cận ngang n ≤ m
Kết quả:
n = m: tiệm cận ngang \(y = \frac{a_n}{b_m}\)
n < m: tiệm cận ngang y = 0
2. Đường tiệm cận đứng
a) x = a được gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện sau
\(\lim_{x\rightarrow a^+} f(x) = \pm \infty\)
\(\lim_{x\rightarrow a^-} f(x) = \pm \infty\)
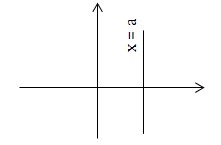
b) Chú ý
+) x = a là đường tiệm cận đứng của đồ thị y = f(x) thì a ∉ TXĐ f(x).
+) Đối với hàm phân thức \(y = \frac{P(x)}{Q(x)}\) thì a là nghiệm Q(x) = 0.
B. Bài tập
VD1: Tìm tiệm cận của đồ thị hàm số \(y=\frac{3x-1}{2x+5}\)
Giải:
\(\lim_{x\rightarrow +\infty } y = \lim_{x\rightarrow +\infty } \frac{3x-1}{2x+5} = \lim_{x\rightarrow +\infty }\frac{3-\frac{1}{x}}{2+\frac{5}{x}} = \frac{3}{2}\)
Vậy \(y = \frac{3}{2}\) là đường tiệm cận ngang.
\(\lim_{x\rightarrow -\frac{5}{2}} y = -\infty\)
Vậy \(x = -\frac{5}{2}\) là đường tiệm cận đứng của đồ thị hàm số.
VD2: Tìm tiệm cận của đồ thị hàm số \(y = \frac{4x + 5}{3x - 1}\)
Giải:
\(\lim_{x \rightarrow -\infty } y = \lim_{x \rightarrow -\infty } \frac{4x + 5}{3x - 1} = \lim_{x \rightarrow -\infty } \frac{4 + \frac{5}{x}}{3-\frac{1}{x} }= \frac{4}{3}\)
Vậy \(y = \frac{4}{3}\) là đường tiệm cận ngang.
\(\lim_{x\rightarrow \frac{1}{3}^-} = - \infty\)
Vậy \(y = \frac{1}{3}\) là đường tiệm cận đứng.
VD3: Tìm tiệm cận ngang của đồ thị hàm số \(f(x) = \frac{2x + 9}{\sqrt{x^2 + 1} + 3x + 5}\)
Giải:
\(\lim_{x\rightarrow +\infty } f(x) = \lim_{x\rightarrow +\infty } \frac{2x + 9}{\sqrt{x^2 + 1} + 3x + 5}\)
\(= \lim_{x\rightarrow +\infty } \frac{2 + \frac{9}{x}}{\sqrt{1+\frac{1}{x^2}} + 3 + \frac{5}{x}}\left ( \frac{\sqrt{x^2 + 1}}{x} = \frac{\sqrt{x^2 + 1}}{\sqrt{x^2}} (\ do\ x > 0)= \sqrt{1 + \frac{1}{x^2}} \right )\)
\(=\frac{2}{4} = \frac{1}{2}\)
Vậy \(y = \frac{1}{2}\) là tiệm cận ngang.
\(\lim_{x\rightarrow -\infty } f(x) = \lim_{x\rightarrow -\infty } \frac{2x + 9}{\sqrt{x^2 + 1} + 3x + 5}\)
\(= \lim_{x\rightarrow -\infty } \frac{2 + \frac{9}{x}}{-\sqrt{1 + \frac{1}{x^2}} + 3 + \frac{5}{x}}\)
\(= \frac{2}{-1 + 3} = 1\)
Vậy y = 1 là tiệm cận ngang.
VD4: Tìm m để đồ thị ham số \(y = \frac{(2m + 3)x + 5}{3x - 1}\) có tiệm cận ngang y = 2.
Giải:
\(\lim_{x\rightarrow +\infty } y = \lim_{x\rightarrow +\infty } \frac{(2m + 3)x + 5}{3x - 1}\)
\(\lim_{x\rightarrow +\infty } \frac{2m + 3 + \frac{5}{x}}{3 - \frac{1}{x}}\)
\(= \frac{2m+3}{3}\)
Vậy \(y= \frac{2m+3}{3}\) là tiệm cận ngang.
y = 2 là đường tiệm cận ngang khi \(\frac{2m+3}{3} = 2\)
⇔ 2m + 3 = 6
⇔ 2m = 3
\(\Leftrightarrow m = \frac{3}{2}\)
VD5: Tìm m để đồ thị hàm số \(y = \frac{4x + 6}{(2m+1)x + 1}\) không có tiệm cận.
Giải:
TH1: \(2m + 1 = 0 \Leftrightarrow m = -\frac{1}{2}\)
Khi đó y = 4x + 6
Vậy \(m = -\frac{1}{2}\) thỏa mãn
TH2: 2m + 1 ≠ 0
\((2m + 1)x + 1 = 0 \Leftrightarrow x = -\frac{1}{2m+1}\)
\(I=\lim_{x \rightarrow {-\frac{1}{2m+1}}^+} \frac{4x + 6}{(2m + 1)x + 1}\)
\(I = \lim_{x \rightarrow {-\frac{1}{2m+1}}^+} (4x + 6) = 4.\left ( -\frac{1}{2m+1} \right ) + 6\)
\(= \frac{-4 + 12m + 6}{2m + 1} = \frac{12m + 2}{2m + 1}\)
12m + 2 ≠ 0 thì \(I = \pm \infty\)
12m + 2 = 0 ⇔ \(m = - \frac{1}{6}\) thì \(y = \frac{4x + 6}{\left ( -\frac{1}{3} + 1 \right )x + 1} = 6\)
\(m = - \frac{1}{6}\) (thỏa mãn)
Vậy \(\left \{ -\frac{1}{2};-\frac{1}{6} \right \}\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



