GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
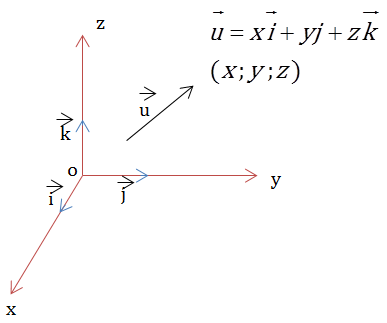
Cho hệ trục tọa độ
Đề các vuông góc Oxyz.
\(\left | \vec{i} \right |=\left | \vec{j} \right |=\left | \vec{k} \right |=1\)
\(\vec{i}\perp \vec{j}, \vec{j}\perp \vec{k}, \vec{i}\perp \vec{k}\)
\(\overrightarrow{u}=(x;y;z)\)
\(\Leftrightarrow \vec{u}=x\vec{i}+y\vec{j}+z\vec{k}\)
\(\vec{u}=(x;y;z)\)
\(\vec{u'}=(x';y'; z')\)
\(\vec{u}+\vec{u'}=(x+x';y+y';z+ z')\)
\(\vec{u}-\vec{u'}=(x-x';y-y';z- z')\)
\(k\vec{u}=(kx;ky;kz)\)
\(\vec{u}=u'\Leftrightarrow \left\{\begin{matrix} x=x'\\ y=y'\\ z=z' \end{matrix}\right.\)
\(\vec{u}=\vec{u'}\) cùng phương \(\Leftrightarrow \left\{\begin{matrix} x=kx'\\ y=ky'\\ z=kz' \end{matrix}\right.\)
\(\left | \vec{u} \right |=\sqrt{x^2+y^2+z^2}\)
II. Bài Tập
VD1: Cho \(\vec{u}=(1;2;3);\vec{v}=(-2;0;1)\)
a) Tính \(\vec{u}+\vec{v}, \left | \vec{u}+\vec{v} \right |\)
b) Tính \(2\vec{u}-\vec{v}, \left | 2\vec{u}-\vec{v} \right |\)
Giải
a)
\(\vec{u}+\vec{v}=(-1;2;4)\)
\(\left | \vec{u}+\vec{v} \right |=\sqrt{(-1)^2+2^2+4^2}=\sqrt{25}=5\)
b)
\(2\vec{u}=(2;4;6)\)
\(\vec{v}=(-2;0;1)\)
\(2\vec{u}-\vec{v}=(4;4;5), \left |2 \vec{u}-\vec{v} \right |=\sqrt{4^2+4^2+5^2}= \sqrt{57}\)
VD2: Cho \(\vec{u}=(2;-1;3), \vec{v}=(-1;0;1),\vec{w}=(0;1;-1)\)
a) Tìm tọa độ \(\vec{x}\) biết \(2\vec{x}+3\vec{u}-\vec{v}=\vec{0}\) (1)
b) Phân tích \(\vec{a}=(3;2;1)\) theo \(\vec{u}, \vec{v}, \vec{w}\)
Giải
a)
\((1)\Leftrightarrow 2\vec{x}=-3\vec{u}+\vec{v}\)
\(\left.\begin{matrix} -3\vec{u}=(-6;3;-9)\\ \vec{v}=(-1;0;1) \end{matrix}\right\} -3 \vec{u} + \vec{v}=(-7;3;-8)\)
\(\Rightarrow 2\vec{x}=(-7;3;-8)\)
\(\Rightarrow \vec{x}=(\frac{-7}{2};\frac{3}{2};-4)\)
b)
Giả sử
\(\vec{a}=m\vec{v}+n\vec{v}+p\vec{w}\)
\(m\vec{u}=(2m;-m;3m)\)
\(n\vec{v}=(-n;0;n)\)
\(p\vec{w}=(0;p;-p)\)
\(\Rightarrow m\vec{u} + n\vec{v}+ p\vec{w} =(2m-n;-m+p;3m+n-p)\)
\(\vec{a}=m\vec{u}+n\vec{v}+p\vec{w}\)
\(\Leftrightarrow \left\{\begin{matrix} 2m-n=3\\ -m+p=2\\ 3m+n-p=1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} n=2m-3\\ p=m+2\\ 3m+2m-3-m-2=1 \ \ (3)\end{matrix}\right.\)
Từ (3) 4m = 6 \(\Leftrightarrow m=\frac{3}{2}\)
Từ (1) n =0
Từ (2) \(p=\frac{7}{2}\)
Vậy \(\vec{a}=\frac{3}{2}\vec{u}+0\vec{v}+\frac{7}{2}\vec{w}\)
VD3: Cho \(\vec{u}=(2;-1;3), \vec{v}=(0;1;-1);\vec{a}=(-1;3;2)\). Tìm đk của m, n để \(\vec{a}\) cùng phương với \(m\vec{u}+n\vec{v}\)
Giải
\(m\vec{u}=(2m;-m;3m)\)
\(n\vec{v}= (0;n;-n)\)
\(\Rightarrow m \vec{u} + n \vec{v}=(2m;- m + n; 3m - n)\)
\(\vec{a}\) cùng phương \(m\vec{u}+n\vec{v}=k.\vec{a}\)
\(\Leftrightarrow \left\{\begin{matrix} 2m=-k\\ -m+n=3k\\ 3m-n=2k \end{matrix}\right.\)
\(+ \ k=0\Rightarrow m=n=0\)
\(+ \ k\neq 0\Rightarrow\left\{\begin{matrix} \frac{2m}{-m+n}=-\frac{1}{3}\\ \\ \frac{3m-n}{2m}=-2 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} 6m=m-n\\ 3m-n=-4m \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} 5m=-n\\ 7m=n \end{matrix}\right.\) (không xảy ra vì \(k\neq 0\) nên \(m\neq 0\))
Vậy m = n = 0














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



