Đề thi tuyển sinh lớp 10 môn Toán trường chuyên năm 2012-2013

Bài 1. (1,5 điểm)

Cho biểu thức: 
1/ Tìm điều kiện của x, y để A(x, y) có nghĩa.
2/ Chứng minh rằng biểu thức A(x, y) không phụ thuộc vào x.

Bài 2. (1,5 điểm)
Cho đường thẳng (D): 
1/ Viết phương trình đường thẳng (d) đi qua A(-3 ; 5) và (d) song song với đường thẳng (D).
2/ Đường thẳng (d) cắt 2 trục tọa độ Ox, Oy lần lượt tại B và C. Tìm các điểm có tọa độ nguyên thuộc đoạn thẳng BC.

Bài 3. (1 điểm)
Giải phương trình sau: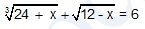

Bài 4. (2 điểm)
Cho phương trình: (*)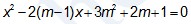
Định m để (*) có 2 nghiệm phân biệt x₁, x₂ sao cho 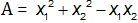 đạt giá trị lớn nhất. Tính giá trị lớn nhất này.

Bài 5. (1 điểm)
Cho tam giác ABC vuông  tại A, vẽ đường cao AH. Chu vi của tam giác ABH bằng 30 cm, chu vi của tam giác ACH bằng 40 cm. Tính chu vi tam giác ABC.

Bài 6 (3 điểm)

Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB, AE và cát tuyến ACD không đi qua tâm O đến đường tròn (O), ở đây B,  E là các tiếp điểm và C nằm giữa A, D
a) Chứng minh AB² = AC. AD
b) Gọi H là giao điểm của BE và AO. Chứng minh tứ giác CHOD nội tiếp được đường tròn.
c) Chứng minh: HB là phân giác của góc CHD.

------ HẾT ------

Cho biểu thức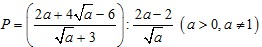
Rút gọn biểu thức P.
Chứng minh rằng P²⁰¹² > 1

Câu 2 (1,0 điểm)
Cho x, y, z là các số dương. Chứng minh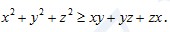 
Dấu “=” xảy ra khi nào ?

Câu 3 (3,0 điểm)
1.  Giải hệ phương trình: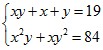 
2. Tìm m nguyên để phương trình sau có ít nhất một nghiệm nguyên: x² + 2mx + 3m² - 8m + 6 = 0

Câu 4 (1,0 điểm)
Cho  không âm, thỏa điều kiện: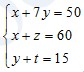
Tìm giá trị lớn nhất của biểu thức A = 2x + y + z + t

Câu 5  (1,0 điểm)
Cho đường tròn (O), dây cung AB (AB < 2R), một điểm M chạy trên cung nhỏ góc AB.Xác định vị trí của để chu vi 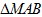 đạt giá trị lớn nhất.

Câu 6  (2,0 điểm)
Cho đường tròn (O; R) vẽ dây cung AB < 2R. Các tiếp tuyến Ax, By của đường tròn (O) cắt nhau tại M. Gọi I là trung điểm của MA và K là giao điểm của BI với (O) 
1. Gọi H là giao điểm của MO và AB. Kẻ dây cung KF đi qua điểm H. Chứng minh rằng MO là tia phân giác của .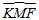
2. Tia MK cắt đường tròn tại điểm C (C khác K). Chứng minh tam giác ABC cân tại A.

-------HẾT-------

Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.

Họ và tên thí sinh: .............................................     Số báo danh: ..............................................
Chữ kí của giám thị 1: .......................................     Chữ kí của giám thị 2: ...............................

Trên đây là 2 đề thi tuyển sinh vào lớp 10 môn Toán của Sở GD&ĐT Kiên Giang và Sở GD&ĐT TP Cần Thơ. Để tham khảo thêm các đề thi của các tỉnh thành khác các em có thể tải tại đây. 
Ngoài việc làm quen với cấu trúc đề thi, các em cần chuẩn bị cho mình một kế hoạch ôn thi với một lộ trình hoàn hảo, cùng HỌC247 tham gia khoá học Luyện thi lớp 10 chuyên để có đạt kết quả thật cao trong kì tuyển sinh sắp đến nhé!

Sưu tầm

• Đề thi Đáp án THPT Quốc gia 2017 môn Toán (22/06)
• Lời giải và bình luận đề thi VMO 2017 (11/01)
• Tuyển chọn các bài toán trong kì thi chọn đội tuyển của các Tỉnh, Thành phố năm học 2016-2017 (22/12)
• Bài tập trắc nghiệm sự tương giao giữa hai đồ thị (14/11)
• Đề thi thử THPT Quốc gia năm 2017 môn Toán trắc nghiệm - THPT Yên Lạc, Vĩnh Phúc Lần 1 (14/11)
• Đề thi thử THPT Quốc gia năm 2017 môn Sinh học - THPT Yên Lạc, Vĩnh Phúc Lần 1 (12/11)
• Đề thi thử THPT Quốc gia năm 2017 môn Giáo dục công dân trường THPT Yên Lạc, Vĩnh Phúc - Lần 1 (12/11)
• Đề thi thử THPT Quốc gia năm 2017 bài thi Khoa học tự nhiên - môn Vật lý - THPT Hàn Thuyên, Bắc Ninh - Lần 1 (12/11)