Câu 1:

Cho z là một số ảo khác 0. Mệnh đề nào sau đây là đúng?

• A. \(z + \overline z = 0\)
• B. \(z=\overline{z}\)
• C. Phần ảo của z bằng 0 
• D. \(\overline{z}\) là số thực

Câu 2:

Giả sử x, y là các số thực dương. Mệnh đề nào sau đây là sai?

• A. \({\log _2}\left( {x + y} \right) = {\log _2}x + {\log _2}y\)
• B. \({\log _2}\sqrt {xy} = \frac{1}{2}\left( {{{\log }_2}x + {{\log }_2}y} \right)\)
• C. \({\log _2}xy = {\log _2}x + {\log _2}y\) 
• D. \({\log _2}\frac{x}{y} = {\log _2}x - {\log _2}y\)

Câu 3:

Cho hàm số \(y = \frac{3}{{x + 1}}\) có đồ thị là (C). Mệnh đề nào sau đây là đúng?

• A. (C) có tiệm cận ngang là y=3.  
• B. (C) có tiệm cận ngang là y=0. 
• C. (C) có tiệm cận đứng là x=1.    
• D. (C) chỉ có một tiệm cận.

Câu 4:

Mệnh đề nào sau đây là đúng?

• A. \(\int {\frac{{dx}}{{\sqrt x }}} = 2\sqrt x + C\)
• B. \(\int {\frac{{dx}}{{{x^2}}} = \frac{1}{x} + C}\)
• C. \(\int {\frac{{dx}}{{x + 1}}} = \ln \left| x \right| + C\)
• D. \(\int {{2^x}dx = {2^x} + C}\)

Câu 5:

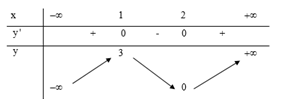
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là sai?

• A. Hàm số đã cho đồng biến trên khoảng \(\left( {2; + \infty } \right).\)  
• B. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;1} \right).\)     
• C. Hàm số đã cho nghịch biến trên khoảng (0;3)   
• D. Hàm số đã cho nghịch biến trên khoảng \(\left( {3; + \infty } \right).\) 

Câu 6:

Tìm tập xác định của hàm số \(y = {\left( {x - 1} \right)^{\frac{1}{2}}}.\)

• A. \(D = \left[ {1; + \infty } \right)\) 
• B. \(D = \left( {1; + \infty } \right)\) 
• C. \(D = \left( { - \infty ;1} \right)\) 
• D. \(D = \left( {0;1} \right)\)

Câu 7:

Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn hàm được đưa ra trong các phương án A, B, C, D dưới đây. Tìm f(x).

• A. \(f\left( x \right) = {x^4} - 2{x^2}\)
• B. \(f\left( x \right) = {x^4} + 2{x^2}\)
• C. \(f\left( x \right) = - {x^4} + 2{x^2} - 1\)
• D. \(f\left( x \right) = - {x^4} + 2{x^2}\)

Câu 8:

Cho phương trình \({z^2} - 2x + 2 = 0.\) Mệnh đề nào sau đây là sai?

• A. Phương trình đã cho không có nghiệm nào là số ảo
• B. Phương trình đã cho có 2 nghiệm phức.
• C. Phương trình đã cho không có nghiệm phức.
• D. Phương trình đã cho không có nghiệm thực.

Câu 9:

 Cho hàm số \(y = \frac{x}{{{2^x}}}\). Mệnh đề nào sau đây là đúng?

• A. Hàm số đã cho có cả điểm cực đại và điểm cực tiểu.
• B. Hàm số đã cho có điểm cực tiểu. 
• C. Hàm số đã cho có điểm cực đại.   
• D. Hàm số đã cho không có điểm cực trị.

Câu 10:

Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và thỏa mãn 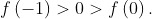 Gọi S là diện tích hình phẳng giới hạn bởi các đường  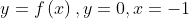và x=1. Mệnh đề nào sau đây đúng?

• A. \(S = \int\limits_{ - 1}^0 {f\left( x \right)dx + \int\limits_0^1 {\left| {f\left( x \right)} \right|dx} }\)
• B. \(S = \int\limits_{ - 1}^1 {\left| {f\left( x \right)} \right|dx}\)
• C. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx}\)
• D. \(S = \left| {\int\limits_{ - 1}^1 {f\left( x \right)dx} } \right|\)

Câu 11:

Tìm điều kiện của tham số m để hàm số \(y = - {x^3} + m{x^2} - x\) có 2 điểm cực trị.

• A. \(\left| m \right| \ge 2\sqrt 3\)
• B. \(\left| m \right| > 2\)
• C. \(\left| m \right| > \sqrt 3\)
• D. \(\left| m \right| \ge \sqrt 3\)

Câu 12:

Trong mặt phẳng với hệ tọa độ Oxy, cho các điểm \(A\left( {0;4} \right),B\left( {1;4} \right),C\left( {1; - 1} \right).\) Gọi G là trọng tâm của tam giác ABC. Biết rằng G là điểm biểu diễn của số phức z. Mệnh đề nào sau đây là đúng?

• A. \(z=2-i\)
• B. \(z = 3 + \frac{3}{2}i\)
• C. \(z=2+i\)
• D. \(z = 3 - \frac{3}{2}i\)

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng 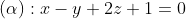 và đường thẳng 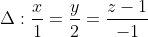. Tìm \(\varphi\) là số đo góc giữa đường thẳng  và mặt phẳng (). 

• A. \(\varphi = {150^0}\)
• B. \(\varphi = {60^0}\)
• C. \(\varphi = {30^0}\)
• D. \(\varphi = {120^0}\)

Câu 14:

 Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^3} - 3}}{{x - 2}}\) trên đoạn \(\left[ { - 1;\frac{3}{2}} \right]\). Mệnh đề nào sau đây là đúng?

• A. \(M + m = \frac{8}{3}\) 
• B. \(M + m = \frac{4}{3}\) 
• C. \(M + m = \frac{7}{2}\) 
• D. \(M + m = \frac{16}{3}\)

Câu 15:

Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và thỏa mãn \(\int\limits_1^e {\frac{{f\left( {\ln x} \right)}}{x}dx} = e.\) Mệnh đề nào sau đây là đúng?

• A. \(\int\limits_0^1 {f\left( x \right)} dx = 1\) 
• B. \(\int\limits_0^1 {f\left( x \right)dx} = e\) 
• C. \(\int\limits_0^e {f\left( x \right)dx} = 1\) 
• D. \(\int\limits_0^e {f\left( x \right)} dx = e\)

Câu 16:

Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Tìm số đo góc ở đỉnh của hình nón.

• A. 150⁰  
• B. 120⁰ 
• C. 60⁰
• D.  30⁰ 

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta\) nằm trong mặt phẳng \(\left( \alpha \right):x + y + z - 3 = 0\) đồng thời đi qua điểm M(1;2;0) và cắt đường thẳng  \(d:\frac{{x - 2}}{2} = \frac{{y - 2}}{1} = \frac{{z - 3}}{1}.\).  Vectơ nào sau đây là một vecto chỉ phương của \(\Delta\).

• A. \(\overrightarrow u = \left( {1; - 1; - 2} \right)\)
• B. \(\overrightarrow u = \left( {1;0; - 1} \right)\)
• C. \(\overrightarrow u = \left( {1;1; - 2} \right)\)
• D. \(\overrightarrow u = \left( {1; - 2;1} \right)\)

Câu 18:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C,\(AB = \sqrt 5 a,AC = a\) . Cạnh SA=3a và vuông góc với mặt phẳng đáy. Tính thể tích V khối chóp S.ABC.

• A. \(V = {a^3}\)
• B. \(V = \frac{{\sqrt 5 }}{2}{a^3}\)
• C. \(V = 2{a^3}\)
• D. \(V = 3{a^3}\)

Câu 19:

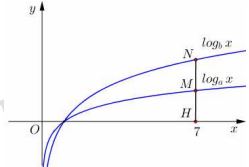
Cho hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên. Đường thẳng x=7 cắt trục hoành, đồ thị hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) lần lượt tại H, M và N. Biết rằng HM=HN. Mệnh đề nào sau đây là đúng?

• A. \(a=7b\)
• B. \(a=b^2\)
• C. \(a=b^7\)
• D. \(a=2b\)

Câu 20:

Tìm tất cả các giá trị của tham số a để đồ thị hàm số \(y = \frac{{{x^2} + a}}{{{x^2} + a{x^2}}}\) có 3 đường tiệm cận.

• A. \(a < 0,a \ne 1\)
• B. \(a> 0\)
• C. \(a \ne 0,a \ne \pm 1\)
• D. \(a \ne 0,a \ne - 1\)

Câu 21:

Tìm tất cả các giá trị của tham số m để hàm số \(y = \frac{1}{{m\log _3^2x - 4{{\log }_3}x + m + 3}}\) xác định trên khoảng \(\left( {0; + \infty } \right).\)

• A. \(m \in \left( { - 4;1} \right)\)
• B. \(m \in \left[ {1; + \infty } \right)\)
• C. \(m \in \left( { - \infty ; - 4} \right) \cup \left( {1; + \infty } \right)\)
• D. \(m \in \left( {1; + \infty } \right)\)

Câu 22:

Gọi \(z_1,z_2\) là các nghiệm phức của phương trình \({z^2} + 2x + 5 = 0\). Tính \(M = \left| {z_1^2} \right| + \left| {z_2^2} \right|.\) 

• A. \(M = 12\)
• B. \(M = 2\sqrt {34}\)
• C. \(M = 4\sqrt 5\)
• D. \(M = 10\)

Câu 23:

Biết rằng \(\int\limits_0^1 {x\cos 2xdx = \frac{1}{4}\left( {a\sin 2 + b\cos 2 + c} \right)}\), với \(a,b,c \in \mathbb{Z}\) Mệnh đề nào sau đây là đúng?

• A. \(a+b+c =1\)
• B. \(a-b+c =0\)
• C. \(a+2b+c =1\)
• D. \(2a+b+c =-1\)

Câu 24:

Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = 0\) và x=4 quanh trục Ox. Đường thẳng x=a (0 tại M (hình vẽ bên). Gọi  là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng \(V = 2{V_1}\). Khẳng định nào sau đây là đúng?

• A. \(a = 2\sqrt 2\)
• B. \(a = \frac{5}{2}\)
• C. \(a = 2\)
• D. \(a = 3\)

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm \(A\left( {2; - 2;5} \right)\) và tiếp xúc với các mặt phẳng \(\left( \alpha \right):x = 1,\left( \beta \right):y = - 1,\left( \gamma \right):z = 1\). Tim bán kính R của mặt cầu (S).

• A. \(R=\sqrt{33}\)
• B.  R=1
• C. \(R=3\sqrt{2}\)
• D. R=3