Câu 1:

Cho hàm số 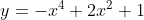. Khẳng định nào sau đây là khẳng định đúng?

• A. Hàm số đồng biến trên khoảng \((0; + \infty ).\)​ 
• B. Hàm số đồng biến trên khoảng \(( - \infty ;0).\)​ 
• C. Hàm số đồng biến trên khoảng \((1; + \infty ).\)​ 
• D. Hàm số đồng biến trên khoảng \(( - \infty ; - 1).\)​ 

Câu 2:

Cho bảng biến thiên như hình vẽ dưới đây:

Khẳng định nào sau đây là khẳng định đúng?

• A. Hàm số giá trị cực đại bằng 3       
• B. Hàm số có giá trị cực đại bằng 2  
• C. Hàm số có giá trị cực đại bằng 1
• D. Hàm số có giá trị cực đại bằng -1 

Câu 3:

Tìm giá trị lớn nhất M của hàm số \(y = {x^2} - 2{x^2} - 4x + 1\) trên đoạn [1; 3].

• A. \(M = - 2.\)
• B. \(M = - 4\).
• C. \(M = \frac{{67}}{{27}}\)
• D. \(M = -7\)

Câu 4:

Cho đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) đạt cực đại tại A(0;3) và cực tiểu B(-1;-5). Tính giá trị của .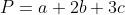

• A. P=-5
• B. P=-9
• C. P=-15
• D. P=3

Câu 5:

Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} + m{x^2} + x + 1\) đồng biến trên R.

• A. \(- 1 < m < 1\)
• B. \(- 1 \le m \le 1\)
• C. \(- 2 < m < 2\)
• D. \(- 2 \le m \le 2\)

Câu 6:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 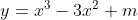 có hai cực trị nằm ở hai nửa mặt phẳng khác nhau với bờ là trục hoành.

• A. 0 < m < 2
• B.  m < 0
• C. m > 2
• D. 0 < m < 4

Câu 7:

Cho hàm số \(y = {x^3} - 3{x^2} + 3\) có đồ thị như hình vẽ:

Tìm tất cả các giá trị thực của tham số m để phương trình \({x^3} - 3{x^2} + m = 0\) có ba nghiệm phân biệt.

• A. \(0 \le m \le 4\)
• B. \(- 4 \le m < 0\)
• C. \(- 4 \le m \le 0\)
• D. \(0 < m < 4\)

Câu 8:

Tìm tất cả các giá trị thực của tham số m để hàm số y = x³ – mx² + (m - 1)x + 1 đồng biến trên khoảng (1; 2).

• A. \(m \le \frac{{11}}{3}\)
• B. \(m < \frac{{11}}{3}\)
• C. \(m \le 2\)
• D. \(m < 2\)

Câu 9:

Một ngọn hải đăng đặt ở vị trí A cách bờ biển một khoảng AB = 4km. Trên bờ biển có 1 cái kho ở vị trí C cách B một khoảng 7km. Người gác ngọn hải đăng chèo thuyền từ ngọn hải đăng đến vị trí M trên bờ biển rồi đi bộ đến C. Biết rằng vận tốc chèo thuyền là 3km/h và vận tốc đi bộ là 5km/h. Xác định vị trí điểm M để người đó đến C nhanh nhất.

• A. MB = 3km
• B. MB = 4 km
• C. M trùng B
• D. M trùng C

Câu 10:

Tìm đạo hàm của hàm số \(y = {\log _2}(x + 1).\)

• A. \(y' = \frac{1}{{(x + 1)ln2}}.\)
• B. \(y' = \frac{{ln2}}{{(x + 1)}}.\)
• C. \(y' = \frac{1}{{x + 1}}.\)
• D. \(y' = \frac{1}{{lo{g_2}(x + 1)}}.\)

Câu 11:

Tìm tập nghiệm S của phương trình \({2^{{x^2} + x - 1}} = \frac{1}{2}.\)

• A. \({\rm{S = \{ - 1;2\} }}{\rm{.}}\)
• B. \({\rm{S = \{ 0;1\} }}{\rm{.}}\)
• C. \({\rm{S = \{ - 1;0\} }}{\rm{.}}\)
• D. \({\rm{S = \{ - 2;1\} }}{\rm{.}}\)

Câu 12:

Tính đạo hàm của hàm số \(y = \sqrt {x\sqrt[3]{x}}\).

• A. \(y' = \frac{{3\sqrt[3]{x}}}{2}\)
• B. \(y' = \frac{3}{{2\sqrt[3]{x}}}\)
• C. \(y' = \frac{{2\sqrt[3]{x}}}{3}\)
• D. \(y' = \frac{2}{{3\sqrt[3]{x}}}\)

Câu 13:

Giải bất phương trình \({\log _{\frac{1}{2}}}(x + 1) > - 3.\)

• A. \(x < 7\)
• B. \(x > 7\)
• C. \(- 1 < x < 8\)
• D. \(- 1 < x < 7\)

Câu 14:

Cho a, b > 0, rút gọn biểu thức \(P = {\log _{\frac{1}{2}}}a + 4{\log _4}b\).

• A. \(P = {\log _2}\left( {\frac{{2b}}{a}} \right)\)
• B. \(P = {\log _2}\left( {{b^2} - a} \right)\)
• C. \(P = {\log _2}\left( {a{b^2}} \right)\)
• D. \(P = {\log _2}\left( {\frac{{{b^2}}}{a}} \right)\)

Câu 15:

Tính tổng S của các nghiệm của phương trình  \(x({2^{x - 1}} + 4) = {2^{x + 1}} + {x^2}\).

• A. S = 7
• B. S = 3
• C. S = 5
• D. S = 6

Câu 16:

Cho các số thực dương a, b thỏa mãn \(\log _9}a = {\log _{12}}b = {\log _{16}}(a + b)\). Tính tỉ số \(T = \frac{a}{b}\).

• A. \(T = \frac{4}{3}\)
• B. \(T = \frac{{1 + \sqrt 3 }}{2}\)
• C. \(T = \frac{{1 + \sqrt 5 }}{2}\)
• D. \(T = \frac{8}{5}\)

Câu 17:

Tìm m để phương trình \(\ln x = m{x^4}\) có đúng một nghiệm biết m là số thực dương.

• A. \(m = \frac{1}{{4e}}\)
• B. \(m = \frac{1}{{4{e^4}}}\)
• C. \(m = \frac{{{e^4}}}{4}\)
• D. \(m = \frac{4}{{\sqrt[4]{e}}}\)

Câu 18:

Tìm tất cả các giá trị thực của tham số m để phương trình 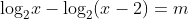 có nghiệm

• A. \(1 \le m < + \infty\)
• B. \(1 < m < + \infty\)
• C. \(0 \le m < + \infty\)
• D. \(0 < m < + \infty\)

Câu 19:

Cho một hình hộp chữ nhật có 3 mặt có diện tích bằng 12, 15 và 20. Tính thể tích của hình hộp chữ nhật đó.

• A. V = 960
• B. V = 20
• C. V = 60
• D. V = 2880

Câu 20:

Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân, AB = AC = a, SA vuông góc với mặt đáy và SA = 2a. Tính thể tích V của khối chóp S.ABC.

• A. \(V = \frac{3}{2}{a^3}\)
• B. \(V = \frac{1}{2}{a^3}\)
• C. \(V = \frac{4}{3}{a^3}\)
• D. \(V = {a^3}\)

Câu 21:

Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh a, SA vuông góc với mặt đáy và SB tạo với mặt đáy một góc 45⁰. Tính thể tích V của hình chóp S. ABC.

• A. \(V = \frac{{\sqrt 3 {a^3}}}{2}\)
• B. \(V = \frac{{\sqrt 3 {a^3}}}{4}\)
• C. \(V = \frac{{\sqrt 3 {a^3}}}{6}\)
• D. \(V = \frac{{\sqrt 3 {a^3}}}{{12}}\)

Câu 22:

Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm đoạn OA. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60⁰. Tính thể tích V của hình chóp S.ABCD.

• A. \(V = \frac{{3\sqrt 3 {a^3}}}{4}\)
• B. \(V = \frac{{\sqrt 3 {a^3}}}{8}\)
• C. \(V = \frac{{\sqrt 3 {a^3}}}{4}\)
• D. \(V = \frac{{\sqrt 3 {a^3}}}{{12}}\)

Câu 23:

Cho một hình lập phương có cạnh bằng a. Tính diện tích mặt cầu nội tiếp hình lập phương đó.

• A. \(S = 4\pi {a^2}\)
• B. \(S = \pi {a^2}\)
• C. \(S = \frac{1}{3}\pi {a^2}\)
• D. \(S = \frac{{4\pi {a^2}}}{3}\)

Câu 24:

Trong không gian cho tam giác ABC vuông tại A có AB = a, AC = 2a. Quay tam giác ABC xung quanh cạnh AB ta được một khối nón. Tính thể tích V của khối nón đó.

• A. \(V = 2\pi {a^3}\)
• B. \(V = \frac{{4\pi {a^3}}}{3}\)
• C. \(V = 4\pi {a^3}\)
• D. \(V = \frac{{2\pi {a^3}}}{3}\)

Câu 25:

Cho một hình nón (N) có góc ở đỉnh bẳng 60⁰ và bán kính đường tròn đáy bằng r₁. Mặt cầu (C) có bán kính r₂ tiếp xúc với mặt đáy và mặt xung quanh của (N). Tính tỉ số \(T = \frac{{{r_2}}}{{{r_1}}}\)

• A. \(T = \frac{1}{{2 + \sqrt 3 }}\)
• B. \(T = \frac{1}{{1 + \sqrt 3 }}\)
• C. \(T = \frac{{\sqrt 3 }}{3}\)
• D. \(T = \frac{1}{2}\)