Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y=x^3-3x^2+2\)
-
Tập xác định: D = R
Ta có

- Hàm số đồng biến trên các khoảngvà
; nghịch biến trên khoảng (0;
 ).
).
- Cực trị: Hàm số đạt cực đại tại x = 0, yCD= 2 ; đạt cực tiểu tại x = 2, yCT =
- Giới hạn:
Bảng biến thiên:
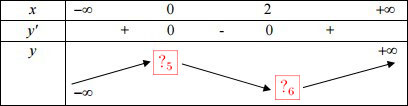
Đồ thị
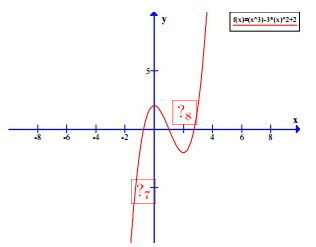
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấu
được ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Tập xác định: D = R
Ta có \(y'=3x^2-6x; y '=0\Leftrightarrow \bigg \lbrack \begin{matrix} x=0\\ x=2 \end{matrix}\)
- Hàm số đồng biến trên các khoảng \((-\infty ;0)\) và \((2;+\infty )\); nghịch biến trên khoảng (0; 2).
- Cực trị: Hàm số đạt cực đại tại x = 0, yCD= 2 ; đạt cực tiểu tại x = 2, yCT = -2
- Giới hạn: \(\lim_{x\rightarrow +\infty }y=+\infty , \lim_{x\rightarrow -\infty }y=-\infty\)
Bảng biến thiên:
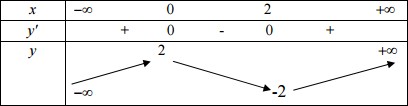
Đồ thị
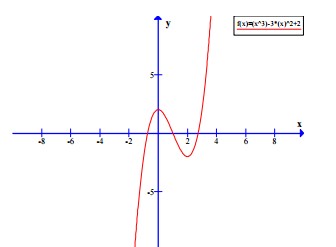
-
-
Câu 2:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(f(x)=\frac{2x+1}{x-1}\) trên đoạn \([3;5]\)
-
Hàm số xác định và liên tục trên
[
 ;
; ]
]
Ta cóDo đó hàm số này nghịch biến trên đoạn [
 ;
; ]
]
Suy ra
f(
 )=
)=
f(
 )=
)=
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Hàm số xác định và liên tục trên \(D=[3;5]\)
Ta có \(f'(x)=-\frac{3}{(x-1)^2}< 0,\forall x\in [3;5]\)Do đó hàm số này nghịch biến trên đoạn [3;5]
Suy ra
\(\underset{x\in [3;5]}{max}f(x)=f(3)=\frac{7}{2}\)
\(\underset{x\in [3;5]}{min}f(x)=f(5)=\frac{11}{4}\) -
-
Câu 3:
a. Cho \(\alpha \left ( \frac{\pi}{2}; \pi \right )\) và \(sin\alpha =\frac{1}{3}\). Tính giá trị biểu thức \(P=sin2\alpha -cos2\alpha\)
b. Giải phương trình: \(sin2x+2sin^2x=sinx+cosx\)-
a.
Vìnên
 , suy ra
, suy ra
Do đó


b.
Phương trình đã cho


với
Vậy phương trình có ba họ nghiệm
với
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
Vì \(\alpha \in \left ( \frac{\pi}{2};\pi \right )\) nên \(cos\alpha < 0\), suy ra \(cos=-\sqrt{1-sin^\alpha }=-\frac{2\sqrt{2}}{3}\)
Do đó \(P=sin 2\alpha - cos 2\alpha = 2sin \alpha cos\alpha - 1 +2sin ^2\alpha\)
\(\Rightarrow P=2.\frac{1}{3}.\left ( -\frac{2\sqrt{2}}{3} \right )-1+2.\left (\frac{1}{3} \right )^2=-\frac{7+4\sqrt{2}}{9}\)
b.
Phương trình đã cho \(\Leftrightarrow 2sinx (sinx+ cosx)= sinx+ cos x\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} sinx+cosx=0 \ \ (1)\\ 2sinx=1 \ \ \ \ \ \ \ \ \ \ (2) \end{matrix}\)
\((1)\Leftrightarrow tanx=-1\Leftrightarrow x=-\frac{\pi}{4}+k\pi, (k\in Z)\)
\((2)\Leftrightarrow sinx=\frac{1}{2}\Leftrightarrow x=\frac{\pi}{6}+k2\pi\vee x=\frac{5\pi}{6}+k2\pi\) với \(k\in Z\)
Vậy phương trình có ba họ nghiệm \(x=-\frac{\pi}{4}+k\pi, x=\frac{\pi}{6}+k2\pi, x=\frac{5\pi}{6}+k2\pi\) với \(k\in Z\) -
-
Câu 4:
Tính tích phân sau: \(I=\int_{0}^{4}2x\left [ 2x^2+ln(x^2+9) \right ]dx\)
-






Vậy

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(I=4\int_{0}^{4}x^3dx+\int_{0}^{4}2xln(x^2+9)dx=I_1+I_2\)
\(I_1=4\int_{0}^{4}x^3dx=x^4 |^4_0=256\)
\(I_2=4\int_{0}^{4}2xln(x^2+9) |^4_0-\int_{0}^{4}2xdx=(x^2+9)ln(x^2+9)|^4_0-x^2|^4_0\)
\(\Rightarrow I_2=25ln25-9ln9-16=50ln5-18ln3-16\)
Vậy \(I=I_1+I_2=240+50ln5-18ln3\)
-
-
Câu 5:
a. Giải bất phương trình: \(log_2(3x-2)-log_2(6-5x)> 0\)
b. Cho tập hợp E= {1;2;3; 4;5;6} và M là tập hợp tất cả các số gồm hai chữ số phân biệt lập từ E. Lấy ngẫu nhiên một số thuộc M. Tính xác suất để tổng hai chữ số của số đó lớn hơn 7.-
a.
Bất phương trình đã cho


Vậy nghiệm của bất phương trình là:

b.
+ Số phần tử của tập M là
+ Các số có tổng hai chữ số lớn hơn 7 gồm: 26, 62, 35, 53, 36, 63, 45, 54, 46, 64, 56, 65. Có số
số
Suy ra xác suất cần tìm là

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
Bất phương trình đã cho \(\Leftrightarrow log_2(3x-2)> log_2(6-5x)\Leftrightarrow \left\{\begin{matrix} 3x-2>0\\ 6-5x>0\\ 3x-2>6-5x \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x>\frac{2}{3}\\ x< \frac{6}{5}\\ x> 1 \end{matrix}\right.\Leftrightarrow 1< x< \frac{6}{5}\)
Vậy nghiệm của bất phương trình là: \(1< x< \frac{6}{5}\)
b.
+ Số phần tử của tập M là \(A_{6}^{2}=30\)
+ Các số có tổng hai chữ số lớn hơn 7 gồm: 26, 62, 35, 53, 36, 63, 45, 54, 46, 64, 56, 65. Có 12 số
Suy ra xác suất cần tìm là \(p=\frac{12}{30}=\frac{2}{5}\) -
-
Câu 6:
Trong không gian với hệ tọa độ (Oxyz), cho các điểm M (1; 2;0), N(3;4;2) và mặt phẳng \((P):2x+2y+z-7=0\). Viết phương trình đường thẳng MN và tính khoảng cách từ trung điểm của đoạn thẳng MN đến mặt phẳng (P).
-
Đường thẳng MN có vectơ chỉ phương

hay

Phương trình đường thẳng MN:(có thể viết dưới dạng pt tham số)
Trung điểm của đoạn thẳng MN là I( ;1;
;1; )
)
Khoảng cách từ I đến mặt phẳng (P) là:
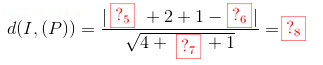
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đường thẳng MN có vectơ chỉ phương \(\overrightarrow{MN}=(-4;6;2)\) hay \(\vec{u}=(-2;3;1)\)
Phương trình đường thẳng MN: \(\frac{x-1}{-2}=\frac{y+2}{3}=\frac{z}{1}\) (có thể viết dưới dạng pt tham số)
Trung điểm của đoạn thẳng MN là I(-1;1;1)
Khoảng cách từ I đến mặt phẳng (P) là:
\(d(I,(P))=\frac{\left | -2+2+1-7 \right |}{\sqrt{4+4+1}}=2\) -
-
Câu 7:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm cạnh AB. Hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm H của CI, góc giữa đường thẳng SA và mặt đáy bằng 600. Tính theo a thể tích khối chóp S.ABC và khoảng cách từ điểm H đến mặt phẳng (SBC).
-
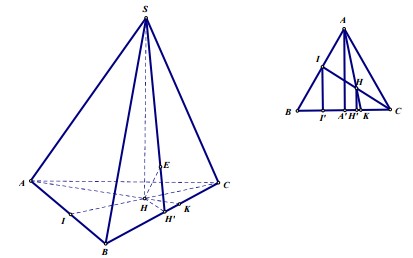
Ta có
Do đó, suy ra

Vậy

Gọi A', H', I' lần lượt là hình chiếu của A, H, I trên BC; E là hình chiếu của H trên SH' thì. Ta có


Từ, suy ra
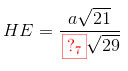
Vậy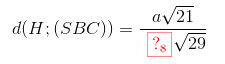
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Ta có \(CI=\sqrt{AC^2-AI^2}=\frac{a\sqrt{3}}{2}\)
Do đó \(AH=\sqrt{AI^2+IH^2}=\frac{a\sqrt{7}}{4}\), suy ra \(SH=AH.tan60^0=\frac{a\sqrt{21}}{4}\)
Vậy \(V_{S.ABC}=\frac{1}{3}.SH.S_{ABC}=\frac{a^3\sqrt{7}}{16}\)
Gọi A', H', I' lần lượt là hình chiếu của A, H, I trên BC; E là hình chiếu của H trên SH' thì \(HE\perp (SBC)\Rightarrow d(H;(SBC))=HE\). Ta có \(HH'=\frac{1}{2}.II'=\frac{1}{4}AA'=\frac{a\sqrt{3}}{8}\)
Từ \(\frac{1}{HE^2}=\frac{1}{HS^2}+\frac{1}{HH'^2}\), suy ra \(HE=\frac{a\sqrt{21}}{4\sqrt{29}}\)
Vậy \(d(H;(SBC))=\frac{a\sqrt{21}}{4\sqrt{29}}\)
-
-
Câu 8:
Trong mặt phẳng với hệ toạ độ Oxy, cho hai đường thẳng \(d_1:3x-4y-8=0,d_2=4x+3y-19=0\). Viết phương trình đường tròn (C) tiếp xúc với hai đường thẳng d1 và d2, đồng thời cắt đường thẳng \(\Delta :2x-y-2=0\) tại hai điểm A B, sao cho AB = \(2\sqrt{5}\).
-
Gọi I (a: b) là tọa độ tâm và R là bán kính đường tròn (C).
Do đường thẳng
cắt đường tròn (C) tại hai điểm A, B sao cho AB =
nên ta có

Đường tròn (C) tiếp xúc với d1, d2 khi:
+ Vớithay vào (*) ta được


Vậy phương trình đường tròn làhoặc

+ Vớithay vào (*) ta được


Vậy phương trình đường tròn là
 hoặc
hoặc 
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Gọi I (a: b) là tọa độ tâm và R là bán kính đường tròn (C).
Do đường thẳng \(\large \Delta\) cắt đường tròn (C) tại hai điểm A, B sao cho AB = \(2\sqrt{5}\) nên ta có
\(d(I,\Delta )=\sqrt{R^2-5}\Leftrightarrow \frac{\left | 2a-b-2 \right |}{\sqrt{5}}=2\sqrt{R^2-5} \ \ (*)\)Đường tròn (C) tiếp xúc với d1, d2 khi: \(\left\{\begin{matrix} d(I,d_1)=R\\ d(I,d_2)=R \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{\left | 3a-4b-8 \right |}{5}=R\\ \\ \frac{\left | 4a+3b-19 \right |}{5}=R \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{\left | 3a-4b-8 \right |}{5}=R\\ \\ 4a+3b-19=\pm (3a-4b-8) \end{matrix}\right.\)\(\Leftrightarrow \Bigg \lbrack\begin{matrix} \left\{\begin{matrix} b=7a-27\\ R=\left | 5a-20 \right | \end{matrix}\right.\\ \left\{\begin{matrix} a=-7b+11\\ R=\left | 5b-5 \right | \end{matrix}\right. \end{matrix}\)
+ Vớithay vào (*) ta được \(\sqrt{5}\left | a-5 \right |=\sqrt{(5a-20)^2-5}\Leftrightarrow a=3\vee a=\frac{9}{2}\)
Vậy phương trình đường tròn là \((C):(x-3)^2+(y+6)^2=25\) hoặc \((C):(x-\frac{9}{2})^2+(y-\frac{9}{2})^2=\frac{25}{4}\)
+ Với \(\left\{\begin{matrix} a=-7b+11\\ R=\left | 5b-5 \right | \end{matrix}\right.\)thay vào (*) ta được \(\sqrt{5}\left | 3b-4 \right |=\sqrt{(5b-5)^2-5}\Leftrightarrow b=2\vee b=\frac{3}{2}\)Vậy phương trình đường tròn là \((C):(x+3)^2+(y-2)^2=25\) hoặc \((C):(x-\frac{1}{2})^2+(y-\frac{3}{2})^2=\frac{25}{4}\)
-
-
Câu 9:
Giải bất phương trình: \(\frac{\sqrt{x+2}-2}{\sqrt{6(x^2+2x+4)}-2(x+2)}\geq \frac{1}{2}\)
-
Điều kiện :

Ta có
Do đó bất phương trình
(1)
Nhận xét x =
 không là nghiệm của bất phương trình
không là nghiệm của bất phương trìnhKhi x > -2 chia hai vế bất phương trinh (1) cho
ta được

(2)
Đặtthì bất phương trình (2) được



Bất phương trình có nghiệm duy nhất
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Điều kiện : \(x\geq\) 2
Ta có \(\sqrt{6(x^2+2x+4)}-2(x+2)=\frac{2(x^2-2x+4)}{\sqrt{6(x^2+2x+4)}+2(x+2)}>0,\forall x\geq -2\)Do đó bất phương trình \(\Leftrightarrow 2(\sqrt{x+2}-2)\geq \sqrt{6(x^2+2x+4)}-2(x+2)\)
\(\Leftrightarrow 2\sqrt{x+2}-2x\geq \sqrt{12(x+2x)+6x^2}\) (1)Nhận xét x = -2 không là nghiệm của bất phương trình
Khi x > -2 chia hai vế bất phương trinh (1) cho \(\sqrt{x+2}> 0\) ta được
\(2+2.\frac{x}{\sqrt{x+2}}\geq \sqrt{12+6.\left ( \frac{x}{\sqrt{x+2}} \right )}\) (2)
Đặt \(t= \frac{x}{\sqrt{x+2}}\) thì bất phương trình (2) được
\(2+2t\geq \sqrt{12+6t^2}\Leftrightarrow \left\{\begin{matrix} 2+2t\geq 0\\ 4+8t+4t^2\geq 12+6t^2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} t\geq -1\\ 2 (t-2)^2\leq 0 \end{matrix}\right.\) \(\Leftrightarrow t=2\)
\(t=2\Leftrightarrow \frac{x}{\sqrt{x+2}}=2\Leftrightarrow \left\{\begin{matrix} x>0\\ x^2-4x-8=0 \end{matrix}\right.\Leftrightarrow x=2+2\sqrt{3}\)
Bất phương trình có nghiệm duy nhất \(x=2+2\sqrt{3}\) -
-
Câu 10:
Cho các số thực dương x, y thỏa mãn điều kiện x + y = 2016 .Tìm giá trị nhỏ nhất của biểu thức
\(P=\sqrt{5x^2+xy+3y^2}+\sqrt{3x^2+xy+5y^2}+\sqrt{x^2+xy+2y^2}+\sqrt{2x^2+xy+y^2}\)-
. Trong đó
và


 (*) dấu đẳng thức xảy ra khi và chỉ khi x = y = 1008
(*) dấu đẳng thức xảy ra khi và chỉ khi x = y = 1008

 (**) dấu đẳng thức xảy ra khi và chỉ khi x = y =
(**) dấu đẳng thức xảy ra khi và chỉ khi x = y = 
Từ (*) và (**) ta đươc , dấu đẳng thức xảy ra khi và chỉ khỉ x = y = 1008
, dấu đẳng thức xảy ra khi và chỉ khỉ x = y = 1008 Vậy

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(P=A+B\). Trong đó
\(A=\sqrt{5x^2+xy+3y^2}+\sqrt{3x^2+xy+5y^2}\) và
\(B=\sqrt{x^2+xy+2y^2}+\sqrt{2x^2+xy+y^2}\)
\(6A=\sqrt{180x^2+36xxy+108y^2}+\sqrt{108x^2+36xy+180y^2}\)
\(=\sqrt{(11x+7y)^2+59(x-y)^2}+\sqrt{(11y+7x)^2+59(y-x)^2}\)
\(\geq (11x+7y)+(11y+7x)=18(x+y)\)
\(\Rightarrow A\geq 3(x+y)=3.2016=6048 \ (*)\) dấu đẳng thức xảy ra khi và chỉ khi x = y = 1008
\(4B=\sqrt{16x^2+16xy+32y^2}+\sqrt{32x^2+16xy+16y^2}\)
\(=\sqrt{(3x+5y)^2+7(x-y)^2}+\sqrt{(3y+5x)^2+7(y-x)^2}\)
\(\geq (3x+5y)+(3y+5x)=8(x+y)\)
\(\Rightarrow B\geq 2(x+y)=2.2016=4032\) (**) dấu đẳng thức xảy ra khi và chỉ khi x = y = 1008
Từ (*) và (**) ta đươc \(P=A+B\geq 6048+4032=10080\), dấu đẳng thức xảy ra khi và chỉ khỉ x = y = 1008Vậy \(P_{min}=10080\Leftrightarrow x=y=1008\)
-





