Câu hỏi trắc nghiệm (9 câu):
-
Câu 1:
Cho hàm số \(y=\frac{2x+1}{x+2}\; \; (1).\)
a. Khảo sát và vẽ đồ thị (C) của hàm số (1).
b. Chứng minh rằng đường thẳng \(d: y = -x + m\) luôn cắt đồ thị (C) tại hai điểm phân biệt A và B. Tìm m để đoạn AB có độ dài nhỏ nhất.
-
a.
- TXĐ: D = R \ {
 }
}- Sự biến thiên:
- Giới hạn - tiệm cận
Ta có:
Suy ra đồ thị hàm số có một tiệm cận đứng là x = -2 và một tiệm cận ngang là y =
 .
.- Chiều biến thiên
Có
Suy ra hàm số đồng biến trên mỗi khoảng
và
- Bảng biến thiên
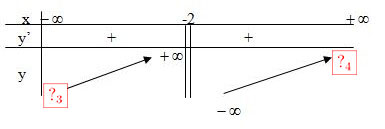
- Đồ thị:
Đồ thị hàm số cắt trục Oy tại điểm

và cắt trục Ox tại điểm

Đồ thị nhận điểm (
 ;
; ) làm tâm đối xứng
) làm tâm đối xứngb. Hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm của phương trình
Do (1) có

và


nên đường thẳng d luôn luôn cắt đồ thị tại hai điểm phân biệt A, B.
Ta có:


nên

mà AB ngắn nhất khi
nhỏ nhất, đạt được khi m =
 (khi đó
(khi đó 
).
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
- TXĐ: D = R \ {-2}
- Sự biến thiên:
- Giới hạn - tiệm cận
Ta có: \(\lim _{x\rightarrow -\infty }y=\lim _{x\rightarrow +\infty }y=2;\lim _{x\rightarrow -2^{+}}y=-\infty ;\lim _{x\rightarrow -2^{-}}y=+\infty\)
Suy ra đồ thị hàm số có một tiệm cận đứng là x = -2 và một tiệm cận ngang là y = 2.
- Chiều biến thiên
Có \(y'=\frac{3}{(x+2)^{2}}>0\; \; \forall x\in D\)
Suy ra hàm số đồng biến trên mỗi khoảng \((-\infty ;-2)\) và \((-2;+\infty)\)
- Bảng biến thiên
- Đồ thị:
Đồ thị hàm số cắt trục Oy tại điểm \((0;\frac{1}{2})\) và cắt trục Ox tại điểm \((-\frac{1}{2};0)\)
Đồ thị nhận điểm (-2; 2) làm tâm đối xứng
b. Hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm của phương trình
\(\frac{2x+1}{x+2}=-x+m\Leftrightarrow \left\{\begin{matrix} \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! x\neq -2\\x^{2}+(4-m)x+1-2m=0\; \; (1) \end{matrix}\right.\)
Do (1) có \(\Delta =m^{2}+1>0\) và \((-2)^{2}+(4-m).(-2)+1-2m=-3\neq 0\;\forall m\) nên đường thẳng d luôn luôn cắt đồ thị tại hai điểm phân biệt A, B.
Ta có: \(y_{A}=m-x_{A};y_{B}=m-x_{B}\) nên \(AB^{2}=(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}=2(m^{2}+12)\) mà AB ngắn nhất khi \(AB^{2}\) nhỏ nhất, đạt được khi m = 0 (khi đó \(AB=\sqrt{24}\)).
-
-
Câu 2:
a. Giải phương trình \(\cos x+\cos 3x=1+\sqrt{2}\sin \left ( 2x+\frac{\pi}{4} \right ).\)
b. Giải phương trình \(\frac{1}{\log _{x}}=\frac{2}{1+\log _{x}}-\frac{1}{6}\)
-
a.




Vậy, phương trình có nghiệm:
b. Điều kiện: x > 0 và

Đặt
được phương trình theo ẩn t là:

(với
và
 )
) Với t = 2 thì ta có x = 100 (t/m)
Với t = 3 thì ta có x = 1000 (t/m)
Vậy phương trình có hai nghiệm là x =
 và x = 1000
và x = 1000Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a. \(\cos x+\cos 3x=1+\sqrt{2}\sin \left ( 2x+\frac{\pi}{4} \right )\)
\(\Leftrightarrow 2\cos x\cos 2x=1+\sin 2x+\cos 2x\)
\(\Leftrightarrow 2\cos ^{2}x+2\sin x\cos x-2\cos x\cos 2x=0\)
\(\Leftrightarrow \cos x(\cos x+\sin x)(1+\sin x-\cos x)=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} \cos x=0\\\cos x+\sin x=0 \\1+\sin x-\cos x=0 \end{matrix}\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x=\frac{\pi}{2}+k\pi\\x=-\frac{\pi}{4}+k\pi \\x=k2\pi \\x=\frac{3\pi}{2}+k2\pi \end{matrix}\; \; (k\in Z)\)
Vậy, phương trình có nghiệm: \(\bigg \lbrack\begin{matrix} x=\frac{\pi}{2}+k\pi\\x=-\frac{\pi}{4}+k\pi \\x=k2\pi \end{matrix}\; (k\in Z)\)
b. Điều kiện: x > 0 và \(x\neq 1;x\neq \frac{1}{10}\)
Đặt \(t=\log x,\) được phương trình theo ẩn t là:
\(t^{2}-5t+6=0\) (với \(t\neq 0\) và \(t\neq -1\)) \(\Leftrightarrow \lbrack\begin{matrix} t=2\\t=3 \end{matrix}\)
Với t = 2 thì ta có x = 100 (t/m)
Với t = 3 thì ta có x = 1000 (t/m)
Vậy phương trình có hai nghiệm là x = 100 và x = 1000
-
-
Câu 3:
Giải bất phương trình \(2.14^{x}+3.49^{x}-4^{x}\geq 0\)
-
Chia cả hai vế của bpt cho
được bpt
Đặt
(với t > 0)
Bpt trở thành




KL: Bpt có tập nghiệm
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=
Lời giải:Chia cả hai vế của bpt cho \(4^{x}\) được bpt \(\Leftrightarrow 2\left ( \frac{7}{2} \right )^{x}+3\left ( \frac{7}{2} \right )^{2x}-1\geq 0\)
Đặt \(t=\left ( \frac{7}{2} \right )^{x}\) (với t > 0)
Bpt trở thành \(3t^{2}+2t-1\geq 0\Leftrightarrow \bigg \lbrack\begin{matrix} t\leq -1\\t\geq \frac{1}{3} \end{matrix}\Rightarrow t\geq \frac{1}{3}\)
\(\Leftrightarrow \left ( \frac{7}{2} \right )^{x}\geq \frac{1}{3}\Leftrightarrow x\geq -\log _{\frac{7}{2}}3\)
KL: Bpt có tập nghiệm \(S=\left [ -\log _{\frac{7}{2}}3;+\infty \right )\)
-
-
Câu 4:
Cho lăng trụ đứng \(ABCA'B'C'\) có \(AC = a, BC = 2a, ACB =120^{\circ}.\) Đường thẳng \(A'C\) tạo với mặt phẳng \((ABB'A')\) góc \(30^{\circ}.\) Gọi \(M\) là trung điểm của \(BB'.\) Tính thể tích khối lăng trụ \(ABCA'B'C'\) và khoảng cách giữa hai đường thẳng \(AM\) và \(CC'\) theo \(a\).
-
Kẻ đường cao CH của tam giác ABC. Có
suy ra
do đó góc giữa A'C và mp (ABB'A') là góc
Ta có


Trong tam giác ABC:

+

+

+

+

+

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Kẻ đường cao CH của tam giác ABC. Có \(CH\perp AB;CH\perp AA'\) suy ra \(CH\perp (ABB'A'),\) do đó góc giữa A'C và mp (ABB'A') là góc \(CA'H=30^{\circ}\)
Ta có \(S_{\triangle ABC}=\frac{1}{2}CA.CB.\sin 120^{\circ}=\frac{a^{2}\sqrt{3}}{2}\)
Trong tam giác ABC: \(AB^{2}=AC^{2}+BC^{2}-2AC.BC.\cos 120^{\circ}=7a^{2}\Rightarrow AB=a\sqrt{7}\)
+ \(S_{\triangle ABC}=\frac{a^{2}\sqrt{3}}{2}=\frac{1}{2}AB.CH\Rightarrow CH=a\sqrt{\frac{3}{7}}\)
+ \(CH=A'C.\sin 30^{\circ}\Rightarrow A'C=2a\sqrt{\frac{3}{7}}\)
+ \(AA'=\sqrt{A'C^{2}-AC^{2}}=a\sqrt{\frac{5}{7}}\)
+ \(V_{ABCA'B'C'}=AA'.S_{\triangle ABC}=\frac{a^{3}\sqrt{15}}{2\sqrt{7}}\)
+ \(d(CC';AM)=d(CC';(ABB'A'))=d(C;(ABB'A'))=a\sqrt{\frac{3}{7}}\)
-
-
Câu 5:
Tìm hệ số của \(x^{7}\) trong khai triển nhị thức Niu-tơn của \(\left ( x^{2}-\frac{2}{x} \right )^{n},\) biết rằng n là số nguyên dương thỏa mãn \(4C^{3}_{n+1}+2C^{2}_{n}=A^{3}_{n}.\)
-
Ta có



Khi đó
Số hạng chứa
là số hạng ứng với k thỏa mãn

Suy ra hệ số của
là

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=
Lời giải:Ta có \(4C^{3}_{n+1}+2C^{2}_{n}=A^{3}_{n}\Leftrightarrow 4.\frac{(n+1)n(n-1)}{6}+n(n-1)=n(n-1)(n-2),n\geq 3\)
\(\Leftrightarrow 2(n+1)+3=3(n-2)\)
\(\Leftrightarrow n=11\)
Khi đó \(\left ( x^{2}-\frac{2}{x} \right )^{11}=\sum_{k-0}^{11}C^{k}_{11}(x^{2})^{11-k}.\left ( -\frac{2}{x} \right )^{k}=\sum_{k-0}^{11}C^{k}_{11}.(-2)^{k}.x^{22-3k}.\)
Số hạng chứa \(x^{7}\) là số hạng ứng với k thỏa mãn \(22-3k=7\Leftrightarrow k=5.\)
Suy ra hệ số của \(x^{7}\) là \(C^{5}_{11}.(-2)^{5}=-14784.\)
-
-
Câu 6:
Tính nguyên hàm \(\int (e^{x}-2015)xdx\)
-
Đặt
Khi đó








Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đặt \(\left\{\begin{matrix} u=x\\dv=(e^{x}-2015)dx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\v=e^{x}-2015x \end{matrix}\right.\)
Khi đó
\(\int (e^{x}-2015)xdx=x(e^{x}-2015x)-\int (e^{x}-2015x)dx\)
\(=xe^{x}-2015x^{2}-(e^{x}-2015.\frac{x^{2}}{2})+C\)
\(=xe^{x}-e^{x}-\frac{2015}{2}x^{2}+C\)
-
-
Câu 7:
Cho hình bình hành ABCD có diện tích bằng 4. Biết A(1; 0), B(0; 2) và giao điểm I của hai đường chéo AC và BD nằm trên đường thẳng y = x. Tìm tọa độ đỉnh C và D.
-
Ta có:

Phương trình của AB là: 2x + y -
 = 0.
= 0.I là trung điểm của AC và BD nên ta có:


Gọi CH là đường cao kẻ từ đỉnh C của hình bình hành
Theo giả thiết

Ta có:
Vậy tọa độ của C và D là
 ;
;
hoặc

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có: \(\overrightarrow{AB}=(-1;2)\Rightarrow AB=\sqrt{5}.\) Phương trình của AB là: 2x + y -2 = 0.
\(I\in (d):y=x\Rightarrow I(t;t).\) I là trung điểm của AC và BD nên ta có:
\(C(2t-1;2t),D(2t;2t-2).\)
Gọi CH là đường cao kẻ từ đỉnh C của hình bình hành
Theo giả thiết \(S_{ABCD}=AB.CH=4\Rightarrow CH=\frac{4}{\sqrt{5}}.\)
Ta có: \(d(C;AB)=CH\Leftrightarrow \frac{\left | 6t-4 \right |}{\sqrt{5}}=\frac{4}{\sqrt{5}}\Leftrightarrow \bigg \lbrack\begin{matrix} t=\frac{4}{3}\Rightarrow C\left ( \frac{5}{3};\frac{8}{3} \right ),D\left ( \frac{8}{3};\frac{2}{3} \right )\\ t=0\Rightarrow C(-1;0),D(0;-2) \end{matrix}\)
Vậy tọa độ của C và D là \(C\left ( \frac{5}{3};\frac{8}{3} \right ),D\left ( \frac{8}{3};\frac{2}{3} \right )\) hoặc \(C(-1;0),D(0;-2)\)
-
-
Câu 8:
Giải hệ phương trình: \(\left\{\begin{matrix} x^{2}+y^{2}+xy+1=4y\\y(x+y)^{2}=2x^{2}+7y+2 \end{matrix}\right.\; \; (x,y\in R).\)
-
NX: Hệ không có nghiệm dạng
Với
ta có:
Đặt
ta có hệ:
.jpg)
+ Với
ta có hệ:
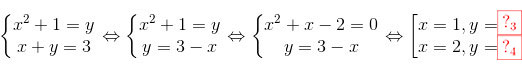
KL: Hệ pt có hai nghiệm là: (1; 2) và (-2; 5).
+ Với
ta có hệ:
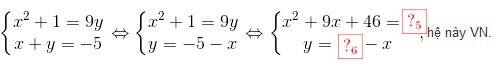
KL: Vậy hệ đã cho có hai nghiệm: (x; y) = {(1;
 ), (-2;
), (-2;  )}.
)}.Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:NX: Hệ không có nghiệm dạng \((x_{0};0)\)
Với \(y\neq 0,\) ta có: \(\left\{\begin{matrix} x^{2}+y^{2}+xy+1=4y\\y(x+y)^{2}=2x^{2}+7y+2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{x^{2}+1}{y}+x+y=4\\(x+y)^{2}-2\frac{x^{2}+1}{y}=7 \end{matrix}\right.\)
Đặt \(u=\frac{x^{2}+1}{y},v=x+y\) ta có hệ:
\(\left\{\begin{matrix} u+v=4\\ v^{2}-2u=7 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} u=4-v\\ v^{2}+2v-15=0 \end{matrix}\right.\Leftrightarrow\bigg \lbrack\begin{matrix} v=3,u=1\\v=-5,u=9 \end{matrix}\)
+ Với \(v=3,u=1\) ta có hệ: \(\left\{\begin{matrix} x^{2}+1=y\\x+y=3 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^{2}+1=y\\y=3-x \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^{2}+x-2=0\\y=3-x \end{matrix}\right.\Leftrightarrow \bigg \lbrack\begin{matrix} x=1,y=2\\x=2,y=5 \end{matrix}.\)
KL: Hệ pt có hai nghiệm là: (1; 2) và (-2; 5).
+ Với \(v=-5,u=9\) ta có hệ: \(\left\{\begin{matrix} x^{2}+1=9y\\x+y=-5 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^{2}+1=9y\\y=-5-x \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^{2}+9x+46=0\\y=-5-x \end{matrix}\right.,\) hệ này VN.
KL: Vậy hệ đã cho có hai nghiệm: (x; y) = {(1; 2), (-2; 5)}.
-
-
Câu 9:
Cho a, b, c là ba cạnh của một tam giác. Chứng minh rằng:
\(a\left ( \frac{1}{3a+b}+\frac{1}{3a+c}+\frac{2}{2a+b+c} \right )+\frac{b}{3a+c}+\frac{c}{3a+b}<2\)
-
Vì a, b, c là ba cạnh tam giác nên:
Đặt
Viết lại vế trái:
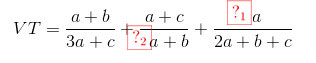
Ta có:

Tương tự:
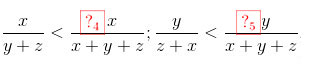
Do đó:
Tức là:
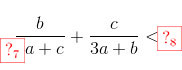
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Vì a, b, c là ba cạnh tam giác nên: \(\left\{\begin{matrix} a+b>c\\b+c>a \\c+a>b \end{matrix}\right..\)
Đặt \(\frac{a+b}{2}=x,\frac{c+a}{2}=y,a=z\; (x,y,z>0)\Rightarrow x+y>z,y+z>x,z+x>y.\)
Viết lại vế trái:
\(VT=\frac{a+b}{3a+c}+\frac{a+c}{3a+b}+\frac{2a}{2a+b+c}\)
\(=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\)
Ta có: \(x+y>z\Leftrightarrow z(x+y+z)<2z(x+y)\Leftrightarrow \frac{2z}{x+y+z}>\frac{z}{x+y}.\)
Tương tự: \(\frac{x}{y+z}<\frac{2x}{x+y+z};\frac{y}{z+x}<\frac{2y}{x+y+z}.\)
Do đó: \(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}<\frac{2(x+y+z)}{x+y+z}=2.\)
Tức là: \(a\left ( \frac{1}{3a+b}+\frac{1}{3a+c}+\frac{2}{2a+b+c} \right )+\frac{b}{3a+c}+\frac{c}{3a+b}<2\)
-




.JPG)
.JPG)
.JPG)
.JPG)

