Câu hỏi trắc nghiệm (9 câu):
-
Câu 1:
Cho hàm số \(y=\frac{x+1}{x-1}(C)\)
a) Khảo sát sự biến thên và vẽ đồ thị (C) của hàm số.
b) Tìm điểm M \(\in (C)\) sao cho tổng khoảng cách từ M đến 2 đường tiệm cận là nhỏ nhất.
-
Cho hàm số
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
Tập xác định: D = R/ {
 }
}Ta có:
Hàm số nghịch biến trên các khoảng
và
Hàm số không có cực trị.
Tính
 nên đồ thị hàm số nhận đường thẳng y = 1 là đường tiệm cận ngang.
nên đồ thị hàm số nhận đường thẳng y = 1 là đường tiệm cận ngang.Tính

 ; nên đồ thị hàm số nhận đường thẳng x = 1 là đường tiệm cận đứng.
; nên đồ thị hàm số nhận đường thẳng x = 1 là đường tiệm cận đứng.Bảng biến thiên:
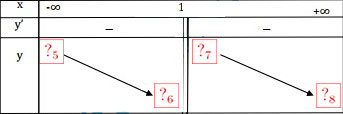
Đồ thị:
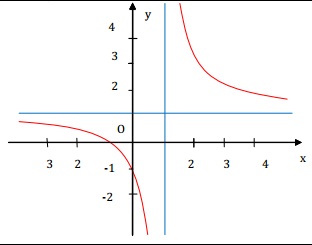
b) Tìm điểm
sao cho tổng khoảng cách từ M đến 2 đường tiệm cận là nhỏ nhất
Gọi M là một điểm thuộc đồ thị hàm số (C), Khi đó

Hai đường tiệm cận của đồ thị là:
và

Ta có khoảng cách từ M đến
là:

Khoảng cách từ M đến
là:
Tổng khoảng cách từ M đến 2 tiệm cận là:

Áp dụng bất đẳng thức Cô-si cho 2 số dương
và
ta có:

, dấu "=" xảy ra khi và chỉ khi

Tương ứng ta có 2 điểm M thỏa mãn là:

và

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Cho hàm số \(y=\frac{x+1}{x-1}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
Tập xác định: D = R/ {1}
Ta có: \(y'=\frac{-2}{(x-1)^{2}}< 0\forall x\in D\)
Hàm số nghịch biến trên các khoảng \((-\infty ;1)\) và \((1;+\infty )\)
Hàm số không có cực trị.
Tính \(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow +\infty }y=1\) nên đồ thị hàm số nhận đường thẳng \(y=1\) là đường tiệm cận ngang.
Tính \(\lim_{x\rightarrow 1^{-}}y=-\infty ; \lim_{x\rightarrow 1^{+}}y=+\infty\); nên đồ thị hàm số nhận đường thẳng x = 1 là đường tiệm cận đứng.
Bảng biến thiên:
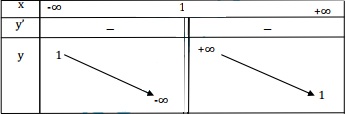
Đồ thị:

b) Tìm điểm \(M\in (C)\) sao cho tổng khoảng cách từ M đến 2 đường tiệm cận là nhỏ nhất
Gọi M là một điểm thuộc đồ thị hàm số (C), Khi đó \(M(a,1+\frac{2}{a-1}).\)
Hai đường tiệm cận của đồ thị là: \((d_{1})x=1,\) và \((d_{2})y=1.\)
Ta có khoảng cách từ M đến \((d_{1})\) là:
\(d(M,d_{1})=\frac{\left | a-1 \right |}{\sqrt{1^{2}+0^{2}}}=\left | a-1 \right |\)
Khoảng cách từ M đến \((d_{2})\) là:
\(d(M,d_{2})=\frac{\left | 1+\frac{2}{a-1} 1\right |}{\sqrt{1^{2}+0^{2}}}=\left | \frac{2}{a-1} \right |\)
Tổng khoảng cách từ M đến 2 tiệm cận là:
\(d(M,d_{1})+d(M,d_{2})=\left | a-1 \right |+\left | \frac{2}{a-1} \right |\)
Áp dụng bất đẳng thức Cô-si cho 2 số dương \(\left | a-1 \right |\) và \(\left | \frac{2}{a-1} \right |\) ta có:
\(\left | a-1 \right |+\left | \frac{2}{a-1} \right |\geq 2\sqrt{2}\), dấu "=" xảy ra khi và chỉ khi
\(\left | a-1 \right |=\left | \frac{2}{a-1} \right |\Leftrightarrow (a-1)^{2}=\left | 2 \right |\Leftrightarrow \bigg \lbrack \begin{matrix}a^{2}-2a+1=2 \\ a^{2}-2a+1=-2 \end{matrix}\Leftrightarrow a=1\pm \sqrt{2}\)
Tương ứng ta có 2 điểm M thỏa mãn là:
\(M_{1}(1+\sqrt{2},1+\sqrt{2})\) và \(M_{2}(1-\sqrt{2},1-\sqrt{2})\)
-
-
Câu 2:
Giải phương trình: \(\cos x+\frac{1}{\cos x}-\frac{3}{2\sin x}=0\)
-
Giải phương trình:
ĐK:
khi đó:
PT







Thỏa mãn điều kiện => họ nghiệm của phương trình là:

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Giải phương trình: \(\cos x+\frac{1}{\cos x}-\frac{3}{2\sin x}=0\)
ĐK: \(\cos x\neq 0, \sin x\neq 0\) khi đó:
PT\(\Leftrightarrow \sin 2x.\cos x+2\sin x-3\cos x=0\)
\(\Leftrightarrow \sin 2x.\cos x-\cos x+2\sin x-2\cos x=0\)
\(\Leftrightarrow (\sin 2x-1).\cos x+2(\sin x-\cos x)=0\)
\(\Leftrightarrow -(\sin x-\cos x)^{2}.\cos x+2(\sin x-\cos x)=0\)
\(\Leftrightarrow (\sin x-\cos x)(2-\cos x(\sin x-\cos x))=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix}\sin x-\cos x=0 \\ 2-\cos x\sin x+\cos ^{2}x=0 \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix}\sqrt{2}\sin (x-\frac{\pi }{4})=0 \\ \frac{2}{\cos^{2}x}-\tan x+1=0 \end{matrix}\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix}\sqrt{2}\sin(x-\frac{\pi }{4})=0 \\ 2(1+\tan ^{2}x)-\tan x+1=0 \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix}\sqrt{2}\sin (x-\frac{\pi }{4})=0 \\2\tan ^{2}x-\tan x+3=0(vn) \end{matrix}\)
\(\Leftrightarrow \sqrt{2}\sin (x-\frac{\pi }{4})=0\)
\(\Leftrightarrow x=\frac{\pi }{4}+k \pi (k\in Z)\)
Thỏa mãn điều kiện => họ nghiệm của phương trình là: \(\Leftrightarrow x=\frac{\pi }{4}+k \pi (k\in Z)\)
-
-
Câu 3:
Tính diện tích hình phẳng được giới hạn bởi các đường sau:
\(y=\ln (x^{2}-x); y=\frac{10}{x}, x=e^{2}\) và \(x=e^{3}\)
-
Diện tích hình phẳng giới hạn bởi
và
được tính theo công thức:
Bây giờ ta đi tính tích phân

Đặt
 x
xVậy





Tiếp tục tính tích phân
Ta có

Vậy diện tích hình phẳng cần tìm là
(đvdt)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Diện tích hình phẳng giới hạn bởi \(y=\ln (x^{2}-x); y=\frac{10}{x}, x=e^{2}\) và \(x=e^{3}\) được tính theo công thức:
\(I=\int_{e^{2}}^{e^{3}}\left | \ln (x^{2}-x)-\frac{10}{x} \right |dx=\left | \int_{e^{2}}^{e^{3}}(\ln (x^{2}-x)-\frac{10}{x})dx \right |\)
\(=\left | \int_{e^{2}}^{e^{3}}\ln (x^{2}-x)dx-\int_{e^{2}}^{e^{3}}\frac{10}{x}dx \right |\)
Bây giờ ta đi tính tích phân \(I_{1}=\int_{e^{2}}^{e^{3}}\ln (x^{2}-x)dx\)
Đặt \(u=\ln (x^{2}-x)\Rightarrow du=\frac{2x-1}{x^{2}-x}dx;dv=dx\Rightarrow v=x\)
Vậy
\(I_{1}=x\ln (x^{2}-x) |_{e^2}^{e^3}-\int_{e^{2}}^{e^{3}}\frac{x(2x-1)}{x(x-1)}dx\)
\(=e^{3}\ln (e^{6}-e^{3})-e^{2}\ln (e^{4}-e^{2})-\int_{e^{2}}^{e^{3}}\frac{2(x-1)+1}{(x-1)}dx\)
\(=e^{3}\ln (e^{6}-e^{3})-e^{2}\ln (e^{4}-e^{2})-2\int_{e^{2}}^{e^{3}}dx-\int_{e^{2}}^{e^{3}}\frac{dx}{x-1}\)
\(=e^{3}\ln (e^{6}-e^{3})-e^{2}\ln (e^{4}-e^{2})-2x |_{e^{2}}^{e^{3}}-\ln \left | x-1 \right | |_{e^{2}}^{e^{3}}\)
\(=e^{3}\ln \left [ e^{3}(e^{3}-1) \right ]-e^{2}\ln \left [ e^{2}(e^{2}-1) \right ]-2e^{3}+2e^{2}-\ln (e^{3}-1)+\ln (e^{2}-1)\)
\(=3e^{3}+e^{3}\ln (e^{3}-1)-2e^{2}-e^{2}\ln (e^{2}-1)-2e^{3}+2e^{2}-\ln (e^{3}-1)+\ln (e^{2}-1)\)
\(=e^{3}+(1-e^{2})\ln (e^{2}-1)-\ln (e^{3}-1)+e^{3}\ln (e^{3}-1)\)
Tiếp tục tính tích phân \(I_{2}=\int_{e^{2}}^{e^{3}}\frac{10}{x}dx\)
Ta có \(I_{2}=\int_{e^{2}}^{e^{3}}\frac{10}{x}dx=10\int_{e^{2}}^{e^{3}}\frac{1}{x}dx=10\ln \left | x \right ||_{e^{2}}^{e^{3}}=10\)
Vậy diện tích hình phẳng cần tìm là
\(I=\left | I_{1}-I_{2} \right |\)
\(=e^{3}+(1-e^{2})\ln (e^{2}-1)+e^{3}\ln (e^{3}-1)-10\) (đvdt)
-
-
Câu 4:
a) Tìm phần thực và phần ảo của các số phức: \(z=\frac{\sqrt{3}-i}{1+i}-\frac{\sqrt{2+i}}{i}\)
b) Cho 8 quả cân trọng lượng lần lượt là: 1 kg, 2 kg,..., 8 kg. Chọn ngẫu nhiên 3 quả cân. Tính xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg.
-
a) Tìm phần thực và phần ảo của các số phức:
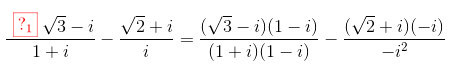

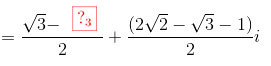
Kết luận:
Phần thực của số phức z là:
Phần ảo của số phức z là:
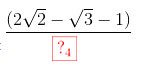
b) Cho 8 quả cân trọng lượng lần lượt là: 1 kg, 2 kg ,…, 8 kg. Chọn ngẫu nhiên 3 quả cân. Tính xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg.
Gọi A là biến cố chọn được 3 quả cân có tổng trọng lượng không vượt quá 9 kg.
Suy ra A có các trường hợp sau:
A = { (1, 2, 3); (1,
 , 4); (1, 2, 5); (1, 2, 6); (1, 3, 4); (1, 3, 5); (
, 4); (1, 2, 5); (1, 2, 6); (1, 3, 4); (1, 3, 5); ( , 3, 4)}
, 3, 4)}
Vậy xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg là:

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a) Tìm phần thực và phần ảo của các số phức: \(z=\frac{\sqrt{3}-i}{1+i}-\frac{\sqrt{2}+i}{i}\)
\(\frac{\sqrt{3}-i}{1+i}-\frac{\sqrt{2}+i}{i}=\frac{(\sqrt{3}-i)(1-i)}{(1+i)(1-i)}-\frac{(\sqrt{2}+i)(-i)}{-i^{2}}\)
\(=\frac{(\sqrt{3}-1)-(\sqrt{3}+1)i}{2}-(1-\sqrt{2}i)\)
\(=\frac{\sqrt{3}-3}{2}+\frac{(2\sqrt{2}-\sqrt{3}-1)}{2}i\)
Kết luận:
Phần thực của số phức z là: \(\frac{\sqrt{3}-3}{2}\)
Phần ảo của số phức z là: \(\frac{(2\sqrt{2}-\sqrt{3}-1)}{2}\)
b) Cho 8 quả cân trọng lượng lần lượt là: 1 kg, 2 kg ,…, 8 kg. Chọn ngẫu nhiên 3 quả cân. Tính xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg.
Gọi A là biến cố chọn được 3 quả cân có tổng trọng lượng không vượt quá 9 kg.
Suy ra A có các trường hợp sau:
A = { (1, 2, 3); (1, 2, 4); (1, 2, 5); (1, 2, 6); (1, 3, 4); (1, 3, 5); (2, 3, 4)}
\(\Rightarrow P=\frac{7}{C^{3}_{8}}=\frac{1}{8}\)
Vậy xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg là: \(\frac{1}{8}\)
-
-
Câu 5:
Cho hình lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh a, cạnh bên tạo với đáy một góc bằng \(30^{\circ}\). Gọi M là trung điểm của BC và I là trung điểm của AM. Biết rằng hình chiếu của điểm I lên mặt đáy A'B'C' là trọng tâm G của \(\Delta A'B'C'\). Tính thể tích khối chóp A.A'B'C' và khoảng cách từ C đến mặt phẳng (ABB'A').
-
Hình vẽ:
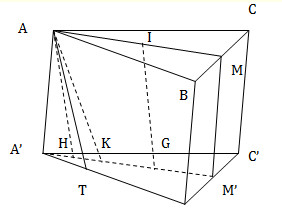
Gọi M' là trung điểm của B'C',
sao cho
Kẻ
Ta có AHGI là hình bình hành nên IG = AH
Hơn nữa AM = A'M'. Gọ I là trung điểm của AM. G là trọng tâm của
Nên H là trung điểm của

Ta có:


Từ đó:

(đvdt)
Ta có:
Từ H kẻ
Khi đó
Ta có:
Tam giác AHT vuông tại H suy ra

Suy ra diện tích của tam giác AB'A' là:


(đvdt)
Ta có

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Hình vẽ:

Gọi M' là trung điểm của B'C', \(K\in A'M'\) sao cho \(A'K=KG=GM'\)
Kẻ \(AH\perp A'M';H\in A'M'\)
Ta có AHGI là hình bình hành nên IG = AH
Hơn nữa AM = A'M'. Gọ I là trung điểm của AM. G là trọng tâm của \(\triangle A'B'C'\)
Nên H là trung điểm của \(A'K\Rightarrow A'H=\frac{1}{6}A'M'\)
Ta có: \(S_{\triangle A'B'C'}=\frac{a^{2}\sqrt{3}}{4};A'M'=\frac{a\sqrt{3}}{2}\Rightarrow A'H=\frac{a\sqrt{3}}{12}\)
\(AH=A'H.\tan 30^{\circ}=\frac{a\sqrt{3}}{12}.\frac{\sqrt{3}}{3}=\frac{a}{12}\)
Từ đó: \(V_{A.A'B'C'}=AH.S_{\triangle A'B'C'}=\frac{1}{3}.\frac{a}{12}.\frac{a^{2}\sqrt{3}}{4}=\frac{a^{3}\sqrt{3}}{144}\) (đvdt)
Ta có: \(d(C,ABB'A')=d(C',ABB'A')\)
Từ H kẻ \(HT\perp A'B',(T\in A'B'),\) Khi đó
\(A'B'\perp HT,AH\perp A'B'\Rightarrow A'B'\perp (AHT)\)
Ta có: \(HT=A'H.\tan 30^{\circ}=\frac{a\sqrt{3}}{12}.\frac{\sqrt{3}}{3}=\frac{a}{12}\)
Tam giác AHT vuông tại H suy ra \(AT=\sqrt{AH^{2}+HT^{2}}=AH\sqrt{2}=\frac{a\sqrt{2}}{12}\)
Suy ra diện tích của tam giác AB'A' là: \(\frac{1}{2}.AT.B'A'=\frac{a^{2}\sqrt{2}}{24}\) (đvdt)
Ta có \(d(C,ABB'A')=d(C',AAB'A')=d(C',AB'A')=\frac{3V_{A.BB'A'}}{S_{AB'A'}}=\frac{1}{4}a\sqrt{6}\)
-
-
Câu 6:
Trong không gian hệ tọa độ Oxyz, cho tứ diện ABCD có các đỉnh A (1; 2; 1), B (-2; 1; 3), C (2; -1; 1) và D (0; 3; 1). Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng khoảng cách từ (D) đến (P).
-
Mặt phẳng (P) thỏa mãn yêu cầu bài toán trong hai trường hợp sau:
Trường hợp 1: (P) qua A, B và song song với CD.
Trường hợp 2: (P) qua A, B và cắt CD. Suy ra (P) cắt CD tại trung điểm I của CD.
Trường hợp 1: (P) qua A, B và song song với CD.
Vec tơ pháp tuyến của (P):


Phương trình (P):
[3]

Trường hợp 2: (P) qua A, B và cắt CD. Suy ra (P) cắt CD tại trung điểm I của CD.


vec tơ pháp tuyến của (P):

Phương trình (P):
 = 0
= 0Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Mặt phẳng (P) thỏa mãn yêu cầu bài toán trong hai trường hợp sau:
Trường hợp 1: (P) qua A, B và song song với CD.
Trường hợp 2: (P) qua A, B và cắt CD. Suy ra (P) cắt CD tại trung điểm I của CD.
Trường hợp 1: (P) qua A, B và song song với CD.
Vec tơ pháp tuyến của (P): \(\overrightarrow{n}=\left [ \overrightarrow{AB},\overrightarrow{CD} \right ]\)
\(\overrightarrow{AB}=(-3;-1;2),\overrightarrow{CD}=(-2;4;0)\Rightarrow \overrightarrow{n}=(-8;-4;-14).\)
Phương trình (P): \(4x+2y+7z-15=0.\)
Trường hợp 2: (P) qua A, B và cắt CD. Suy ra (P) cắt CD tại trung điểm I của CD.
\(I(1;1;1)\Rightarrow \overrightarrow{AI}=(0;-1;0);\) vec tơ pháp tuyến của (P): \(\overrightarrow{n}=\left [ \overrightarrow{AB},\overrightarrow{AI} \right ]=(2;0;3).\)
Phương trình (P): \(2x+3z-5=0\)
Kết luận: Vậy (P): \(4x+2y+7z-15=0\) hoặc (P): \(2x+3z-5=0.\)
-
-
Câu 7:
Cho \(\triangle ABC\) có trung điểm cạnh BC là \(M(3;-1)\), đường thẳng chứa đường cao kẻ từ B đi qua điểm \(E(-1; -3)\) và đường thẳng chứa AC đi qua điểm \(F(1;3)\). Điểm đối xứng của đỉnh A qua tâm đường tròn ngoại tiếp \(\triangle ABC\) là điểm \(D(4;-2)\). Tìm tọa độ đỉnh A của \(\triangle ABC\) và phương trình đường thẳng BC.
-
Hình vẽ:
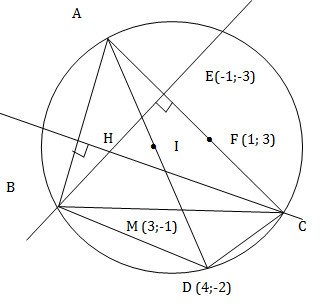
Gọi H là trực tâm ΔABC thì có BHCD là hình bình hành, nên M là trung điểm HD => H (
 ; 0)
; 0)BH chứa
nên (BH):

Do DC // BH và D (4; -2) thuộc DC nên (DC):
Do BH
AC và F (1; 3) thuộc AC nên (AC):

Do
nên tọa độ C là nghiệm của hệ
Tìm được C (
 ; -1)
; -1)M (3; -1) là trung điểm của BC nên B (1; -1) =>
Từ đây ta suy ra phương trình đường thẳng BC là: y =

Do H là trực tâm ΔABC nên AH
BC => (AH): x –
 = 0
= 0Do A = AH ∩ AC nên tọa độ A là nghiệm của hệ

Kết luận: A (2; 2), phương trình BC: y=

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Hình vẽ:

Gọi H là trực tâm ΔABC thì có BHCD là hình bình hành, nên M là trung điểm HD => H (2; 0)
BH chứa \(E(-1;-3)\) nên (BH): \(\frac{x-2}{-1-2}=\frac{y-0}{-3-0}\Leftrightarrow (BH):x-y-2=0\)
Do DC // BH và D (4; -2) thuộc DC nên (DC): \(x-y-6=0\)
Do BH \(\perp\) AC và F (1; 3) thuộc AC nên (AC): \(x+y-4=0\)
Do \(C=AC\cap DC\) nên tọa độ C là nghiệm của hệ \(\left\{\begin{matrix}x-y-6=0 \\x+y-4=0 \end{matrix}\right.\)
Tìm được C (5; -1)
M (3; -1) là trung điểm của BC nên B (1; -1) => \(\overrightarrow{BC}=(4;0)\)
Từ đây ta suy ra phương trình đường thẳng BC là: y = -1
Do H là trực tâm ΔABC nên AH \(\perp\) BC => (AH): x – 2 = 0
Do A = AH ∩ AC nên tọa độ A là nghiệm của hệ \(\left\{\begin{matrix}x-2=0 \\x+y-4=0 \end{matrix}\right.\Rightarrow A(2;2)\)
Kết luận: A (2; 2), phương trình BC: y= -1
-
-
Câu 8:
Giải hệ phương trình: \(\left\{\begin{matrix}x^{2}(x-3)-y\sqrt{y+3}=-2 \\ 3\sqrt{x-2}=\sqrt{y(y+8)} \end{matrix}\right.\)
-
Điều kiện:
Ta có:


Với hàm số
Xét hàm số
với
có

Hàm số
đồng biến trên
Nên từ
Từ

 (*)
(*)

Với điều kiện
thì
=> PT (*) có nghiệm duy nhất là y = 1
Với y = 1 => x =

Kết luận: Hệ có nghiệm duy nhất: (3; 1)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Điều kiện: \(\left\{\begin{matrix}y+3\geq 0 \\y^{2}+8y\geq 0 \\ x-2\geq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x\geq 2 \\ y\geq 0 \end{matrix}\right.\)
Ta có: \(x^{2}(x-3)-y\sqrt{y+3}=-2\)
\(\Leftrightarrow x^{3}-3x^{3}+2=\sqrt{y^{3}+3y^{2}}\)
\(\Leftrightarrow (x-1)^{3}-3(x-1)=(\sqrt{y+3})^{3}-3\sqrt{y+3}\)
\(\Leftrightarrow f(x-1)=f(\sqrt{y+3})\) Với hàm số \(f(t)=t^{3}-3t\)
Xét hàm số \(f(t)=t^{3}-3t\) với \(t\in \lbrack 1;+\infty )\) có \(f'(t)=3t^{2}-3=3(t^{2}-1)\geq 0\)
Hàm số \(f(t)=t^{3}-3t\) đồng biến trên \(\lbrack 1;+\infty )\)
Nên từ \(f(x-1)=f(\sqrt{y+3})\Rightarrow x-1=\sqrt{y+3}\Leftrightarrow x-2=\sqrt{y+3}-1\)
Từ \(3\sqrt{x-2}=\sqrt{y^{2}+8y}\Rightarrow 9(x-2)=y^{2}+8y\)
\(\Leftrightarrow 9(\sqrt{y+3}-1)=y^{2}+8y\)
\(\Leftrightarrow 9\sqrt{y+3}=y^{2}+8y+9\) (*)
\(\Leftrightarrow 9(\sqrt{y+3}-2)=y^{2}+8y-9\)
\(\Leftrightarrow 9\frac{y-1}{\sqrt{y+3}+2}=(y-1)(y+9)\)
\(\Leftrightarrow (y-1)(\frac{9}{\sqrt{y+3}+2}-y-9)= 0\)
Với điều kiện \(y\geq 0,\) thì \(\frac{9}{\sqrt{y+3}+2}-y-9< 0\)
=> PT (*) có nghiệm duy nhất là y = 1
Với y = 1 => x = 3
Kết luận: Hệ có nghiệm duy nhất: (3; 1)
-
-
Câu 9:
Cho các số thực dương a, b, c thỏa mãn a+b+c = 3. Chứng minh rằng:
\(\frac{a^{3}+b^{3}}{3a^{2}-4ab+11b^{2}}+\frac{b^{3}+c^{3}}{3b^{2}-4bc+11c^{2}}+\frac{c^{3}+a^{3}}{3c^{2}-4ac+11a^{2}}\geq \frac{3}{5}\)
-
Ta xét hàm số:

ta có
Dự đoán dấu "=" xảy ra khi a = b = c =

=> Xét

Có phương trình tiếp tuyến tại t =
 là:
là: 
Nhận thấy:



=> Điều phải chứng minh.
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta xét hàm số: \(f(t)=\frac{t^{3}+1}{3t^{2}-4t+11};t\in (0;3]\) ta có \(f'(t)=\frac{3t^{4}-8t^{3}+33t^{2}-6t+4}{(3t^{2}-4t+11)^{2}}\)
Dự đoán dấu "=" xảy ra khi a = b = c = 1
=> Xét \(f'(1)=\frac{13}{50}\)
Có phương trình tiếp tuyến tại t = 1 là: \(y(t)=\frac{13}{50}t-\frac{3}{50}\)
Nhận thấy:
\(f(t)-y(t)=\frac{t^{3}+1}{3t^{2}-4t+11}-\frac{13}{50}t+\frac{3}{50}\)
\(\frac{-(t-1)^{2}(11t+81)}{50(3t^{2}-4t+11)}\geq 0,\forall t\in (0;3]\)
\(\Rightarrow \frac{t^{3}+1}{3t^{2}-4t+11}\geq \frac{13}{50}t-\frac{3}{50},\forall t\in (0;3]\)
\(t=\frac{a}{b}\Rightarrow \frac{a^{3}+b^{3}}{3a^{2}-4ab+11b^{2}}\geq \frac{13a-3b}{50}\)
\(t=c\Rightarrow \frac{b^{3}+c^{3}}{3b^{2}-4bc+11c^{2}}\geq \frac{13b-3c}{50}\)
\(t=\frac{a}{b}\Rightarrow \frac{c^{3}+a^{3}}{3c^{2}-4ac+11a^{2}}\geq \frac{13c-3a}{50}\)
\(\Rightarrow VT\geq \frac{1}{5}(a+b+c)=\frac{3}{5}\)
=> Điều phải chứng minh.
-





