Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
Cho hàm số \(\small y=f(x)=\frac{2x+1}{x-1}\ \ (1)\)
a). Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
b). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M thuộc (C) và có tung độ bằng 3.-
a).
+ Tập xác định: D = R \ {
 }
}+ Giới hạn và tiệm cận:

Tiệm cậ
n ngang
 .
.

Tiệm cận đứng

+ Sự biến thiên:
- Chiều biến thiên:
.
Hàm số nghịch biến trên từng khoảng
và
- Cực trị: Hàm số không có cực trị
- Bảng biến thiên
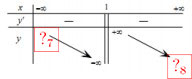
Đồ thị: (0,25đ)
.png)
b).
+ Gọi M
ta có
là nghiệm của phương trình
 Suy ra M(4;
Suy ra M(4; )
) + Ta có
Hệ số góc của tiếp tuyến là


+ Phương trình tiếp tuyến của (C) tại M(
 ;3):
;3): 
+ Vậy phương trình tiếp tuyến cần tìm là


Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
= - Chiều biến thiên:
Lời giải:a).
+ Tập xác định: D = R \ {1}
+ Giới hạn và tiệm cận:
\(\lim_{x\rightarrow -\infty }y = \lim_{x\rightarrow +\infty }y = 2 \Rightarrow\) Tiệm cậ
n ngang \(y = 2\).
\(\lim_{x\rightarrow 1}=y=-\infty ; \lim_{x\rightarrow 1}=y=+\infty \Rightarrow\) Tiệm cận đứng \(x=1.\)
+ Sự biến thiên:
- Chiều biến thiên: \(y'=\frac{-3}{(x-1)^{2}}; y'<0,\forall x\in D\).
Hàm số nghịch biến trên từng khoảng \((-\infty ;1)\) và \((1;+\infty ).\)
- Cực trị: Hàm số không có cực trị
- Bảng biến thiên (0,25đ)
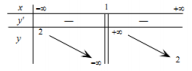
- Đồ thị: (0,25đ)
.png)
b).
+ Gọi M\((x_0;3)\in (C)\) ta có \(x_0\) là nghiệm của phương trình
\(\frac{2_{x_0}+1}{_{x_0}-1}=3 \Leftrightarrow \left\{\begin{matrix}x_0 \neq 1 \\ 2x_0+1=3(x_0-1) \end{matrix}\right. \Leftrightarrow x_0 =4.\) Suy ra M(4;3)
+ Ta có \(f'(x)=\frac{-3}{(x-1)^{2}}\Rightarrow\) Hệ số góc của tiếp tuyến là \(f'(4)=\frac{-3}{(4-1)^{2}}=-\frac{1}{3}\)
+ Phương trình tiếp tuyến của (C) tại M(4;3): \(y=-\frac{1}{3}(x-4)+3\)
+ Vậy phương trình tiếp tuyến cần tìm là \(y=-\frac{1}{3}x + \frac{13}{3}\)
-
-
Câu 2:
a) Cho \(\small 0< x< \frac{\pi}{4}\) và \(\small x-y=\frac{3\pi}{4}\). Tính giá trị của biểu thức \(\small A=(1-tanx)(1+tany)\)
b) Tìm số phức z và tính mô đun z, biết \(\small (3+i)\overline{z}+(1+i)(2-i)=5-i\)-
a)
+ Ta cóvà

+ Khi đó:


b)
+ Giả sửta có



Vậy

và
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a)
+ Ta có \(x=\frac{3\pi }{4}+y\) và \(tanx=\left ( \frac{3\pi }{4}+4 \right )=\frac{tan\frac{3\pi }{4}+tany}{1-tan\frac{3\pi }{4}tany}=\frac{-1+tany}{1+tany}\)
+ Khi đó: \(A=\left [ 1-(\frac{-1+tany}{1+tany}) \right ](1+tany)=1+tany+1-tany=2\)
b)
+ Giả sử \(z=a+bi(a,b\in R)\) ta có \((1)\Leftrightarrow (3+i)(a-bi)=2-2i\)
\(\Leftrightarrow (3a+b)(a-3b)i=2-2i\)
\(\Leftrightarrow\left\{\begin{matrix} 3a+b=2\\ a-3b=-2 \end{matrix}\right. \Leftrightarrow\left\{\begin{matrix} a=\frac{2}{5}\\ b=\frac{4}{5} \end{matrix}\right.\)Vậy \(z=\frac{2}{5}+\frac{4}{5}i\) và \(\left | z \right |=\frac{2\sqrt{5}}{5}\)
-
-
Câu 3:
Giải phương trình \(\small log_3(x^2+3x)+log_\frac{1}{3}(2x+2)=0\)
-
(1)
+ ĐK:
Ta có (1)





Kết hợp với điều kiện (*), ta có nghiệm của phương trình là x =
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(\small log_3(x^2+3x)+log_\frac{1}{3}(2x+2)=0\) (1)
+ ĐK: \(\left\{\begin{matrix} x^2+3x> 0\\ 2x+2> 0 \end{matrix}\right.\Leftrightarrow x> 0 \ \ (*)\)
Ta có (1) \(\Leftrightarrow log_3(x^2+3x)-log_3(2x+2)=0\Leftrightarrow log_3(x^2+3x)=log_3(2x+2)\)
\(\Leftrightarrow x^2+3x=2x+2\Leftrightarrow x^2+x-2=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=1\\ x=-2 \end{matrix}\)
Kết hợp với điều kiện (*), ta có nghiệm của phương trình là x = 1 -
-
Câu 4:
Giải phương trình \(\small 2x+5>\sqrt{2-x}(\sqrt{x-1}+\sqrt{3x+4})\)
-
+ ĐK:
 . Ta có
. Ta có
(1) trở thành
+ Do
nên

So với điều kiện và suy ra tập nghiệm của bất phương trình là
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=
Lời giải:+ ĐK: \(1\leq x\leq 2\). Ta có \(2x+5=3x+4-(x-1)=(\sqrt{3x+4}+\sqrt{x-1})(\sqrt{3x+4}-\sqrt{x-1})\)
(1) trở thành \((\sqrt{3x+4}+\sqrt{x-1})(\sqrt{3x+4}-\sqrt{x-1})> \sqrt{2-x}(\sqrt{x-1}+\sqrt{3x+4}) \ \(2)\)
+ Do \(\sqrt{x-1}+\sqrt{3x+4}> 0\forall x\in \left [ 1;2 \right ]\) nên
\((2)\ \ \Leftrightarrow \sqrt{3x+4}-\sqrt{x-1}> \sqrt{2-x}\Leftrightarrow \sqrt{3x+4}> \sqrt{2-x}+\sqrt{x-1}\)
\(\Leftrightarrow 3x+3> 2\sqrt{(2-x)(x-1)}\)
\(\Leftrightarrow \sqrt{-x^2+3x-2}< \frac{3x+3}{2}\Leftrightarrow \left\{\begin{matrix} \frac{3x+3}{2}> 0\\ -x^2+3x-2\geq 0\\ -x^2+3x-2< (\frac{3x+3}{2})^2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x> -1\\ 1\leq x\leq 2\\ 13x^2+17 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 1\leq x\leq 2\\ x\in R \end{matrix}\right.\Leftrightarrow 1\leq x\leq 2\)
So với điều kiện và suy ra tập nghiệm của bất phương trình là \(S=\left [ 1;2 \right ]\) -
-
Câu 5:
Tính tích phân \(\small I=\int_{e}^{e^2}(1+lnx)xdx\)
-
+ Ta có:
+ Tính

+ Tính
. Đặt
Ta có


+ Vậy

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:+ Ta có: \(I=\int_{e}^{e^2}xdx+\int_{e}^{e^2}xlnxdx=I_1+I_2 \ \ (1)\)
+ Tính \(I_1=\int_{e}^{e^2}xdx=\frac{1}{2}x^2\big|_{e}^{e^2}=\frac{1}{2}(e^4-e^2)\)
+ Tính \(I_2=\int_{e}^{e^2}x\ lnx \ dx\). Đặt \(\left\{\begin{matrix} u=lnx\\ dv=xdx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} u'=\frac{1}{x}\\ v=\frac{x^2}{2} \end{matrix}\right.\)
Ta có \(I_2=\left ( \frac{x^2}{2}lnx \right )\big|_{e}^{e^2}-\int_{e}^{e^2}x dx\)
\(=\left ( \frac{x^2}{2}lnx \right )\big|_{e}^{e^2}-\left ( \frac{1}{4} x^2\right )\big|_{e}^{e^2}=\frac{1}{2}(2e^4-e^2)=\frac{3e^4-e^2}{4}\)
+ Vậy \((1)\Rightarrow I=I_1+I_2=\frac{e^4-e^2}{2}+\frac{3e^4-e^2}{4}=\frac{5e^4-3e^2}{4}=\frac{e^2(5e^2-3)}{4}\) -
-
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, BC = 2a. Tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, mặt bên (SAC) hợp với mặt đáy một góc 600. Tính theo a thể tích khối chóp S.ABC và khoảng cách từ điểm A đến mặt phẳng (SCI), biết rằng I là trung điểm của cạnh AB.
-
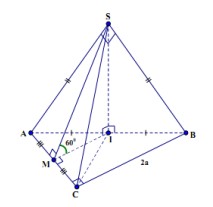
+ Ta có ∆SAB vuông cân tại S, I là trung điểm ABSI
AB và (SAB)
(ABC)
SI
(ABC). Gọi M là trung điểm AC, ta có IM // BC,

và
do SI
(ABC))
SM
AC (định lý 3 đường vuông góc)
 là góc giữa hai mặt phẳng (SAC) và (ABC).
là góc giữa hai mặt phẳng (SAC) và (ABC).
+SMI vuông tại I,


;
SAB vuông cân tại S
ABC vuông tại C

. Do đó
+ Ta có
+ Mặt khác
Suy ra
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
+ Ta có ∆SAB vuông cân tại S, I là trung điểm AB \(\Rightarrow\) SI \(\perp\) AB và (SAB) \(\perp\) (ABC)
\(\Rightarrow\) SI \(\perp\) (ABC). Gọi M là trung điểm AC, ta có IM // BC, \(IM=\frac{1}{2}BC=a\Rightarrow IM\perp AC\) và \(IM\perp SI\) do SI \(\perp\) (ABC)) \(\Rightarrow\) SM \(\perp\) AC (định lý 3 đường vuông góc) \(\Rightarrow\) \(\widehat{SMI}=60^0\)là góc giữa hai mặt phẳng (SAC) và (ABC).
+ \(\Delta\)SMI vuông tại I, \(\widehat{SMI}=60^0\Rightarrow SI=IM.tan60^0=a\sqrt{3}\); \(\Delta\)SAB vuông cân tại S
\(\Rightarrow AB=2SI=2\sqrt{3}a;\) \(\Delta\)ABC vuông tại C \(\Rightarrow AC=\sqrt{AB^2-BC^2}=2\sqrt{2}a\). Do đó \(V_{S.ABC}=\frac{1}{3}.S_{ABC}.SI=\frac{2\sqrt{6}}{3}a^3\)
+ Ta có \(d(A;(SCI))=\frac{3V_{A.SCI}}{S_{SCI}};V_{A.SCI}=V_{S.ACI}=\frac{1}{2}V_{S.ABC}=\frac{\sqrt{6}}{3}a^3\)
+ Mặt khác \(SI \perp (ABC), IC \subset (ABC) \Rightarrow SI \perp IC \Rightarrow S_{SCI}=\frac{1}{2}IC.SI\)
\(=\frac{1}{2}\left ( \frac{AB}{2} \right )SI=\frac{3}{3}a^2\)
Suy ra \(d(A,(SCI))=\frac{3V_{A.SCI}}{\frac{3a^2}{2}}=\frac{2\sqrt{6}}{3}a\) -
-
Câu 7:
Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang ABCD có \(\small \widehat{BAD}=\widehat{ADC}=90^0\), AD = 2, DC = 4, đỉnh C nằm trên đường thẳng d: 3x – y + 2 = 0. Diểm M nằm trên cạnh AD sao cho AM = 2MD và đường thẳng BM có phương trình là 3x – 2y + 2 = 0. Tìm tọa độ của đỉnh C.
-
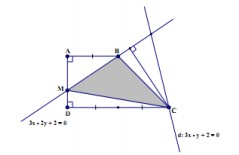
+ Ta có
(1)
+ Theo giả thiết: và
và 
ABM vuông cân tại A
CDM vuông tại D
và


+ABM vuông cân tại A
và ta lại có

(2)
+ Từ (1) và (2) ta có
Suy ra: C= (-4; -10) hoặc C=( ;10).
;10).Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
+ Ta có \(C\in d\left\{\begin{matrix} x=t\\ y=2+3t \end{matrix}\right.(t\in R)\Rightarrow C(t;2+3t)\Rightarrow d(C,BM)=\frac{\left | 3x_C-2y_C+2 \right |}{\sqrt{3^2+(-2)^2}}\)
\(=\frac{\left | 2+3t \right |}{\sqrt{13}}\) (1)
+ Theo giả thiết: \(M\in AD,AM=2MD\Rightarrow MD=\frac{1}{3}AD=\frac{2}{3}\) và \(AM=\frac{4}{3}\)
\(\Delta\)ABM vuông cân tại A \(\Rightarrow S_{ABM}=\frac{1}{2}AM.AB=\frac{4}{3}\) \(\Delta\)CDM vuông tại D
\(\Rightarrow S_{MCD}=\frac{1}{2}MD.DC=\frac{4}{3}\) và \(S_{ABCD}=\frac{1}{2}(AB+CD)AD=6\)
\(\Rightarrow S_{BMC}=S_{ABCD}-S_{ABM}-S_{MDC}=\frac{10}{3}\)
+ \(\Delta\)ABM vuông cân tại A \(\Rightarrow BM=\sqrt{AB^2+AM^2}=\sqrt{4+\frac{16}{9}}=\frac{2\sqrt{13}}{3}\) và ta lại có
\(S_{BMC}=\frac{1}{2}BM.d(C,BM)\Leftrightarrow d(C,BM)=\frac{2.S_{BMC}}{BM}=\frac{2.(\frac{10}{3})}{\frac{2\sqrt{13}}{3}}=\frac{10}{\sqrt{13}}\) (2)
+ Từ (1) và (2) ta có \(\frac{\left | 2+3t \right |}{\sqrt{13}}=\frac{10}{\sqrt{13}}\Leftrightarrow \left | 2+3t \right |=10\Leftrightarrow \bigg \lbrack\begin{matrix} 2+3t=10\\ 2+3t=-10 \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix} t=\frac{8}{3}\\ t=-4 \end{matrix}\)
Suy ra: C= (-4; -10) hoặc C=(\(\frac{8}{3}\);10). -
-
Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;3;-2) và mặt phẳng (P) có phương trình 2x – y + 2z – 1 =0. Viết phương trình mặt cầu (S) có tâm là A và tiếp xúc với (P). Tìm tọa độ của tiếp điểm.
-
+ Vì mặt cầu (S) tâm A tiếp xúc với (P) nên bán kính của (S) là

+ Suy ra

+ Goi d là đường thẳng qua A và vuông góc với (P). Gọi K là giao điểm của d và (P), ta có K là tiếp điểm của (P) và (S). Ta có một véc tơ chỉ phương d là
và phương trình tham số của

vì
+ Mặt khác

 suy ra
suy ra Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:+ Vì mặt cầu (S) tâm A tiếp xúc với (P) nên bán kính của (S) là
\(R=d(A,(P))=\frac{\left | 2.1-3+2(-2)-1 \right |}{\sqrt{4+1+4}}=2\)
+ Suy ra \((S): (x-1)^2+(y-3)^2+(z+2)^2=4\)
+ Goi d là đường thẳng qua A và vuông góc với (P). Gọi K là giao điểm của d và (P), ta có K là tiếp điểm của (P) và (S). Ta có một véc tơ chỉ phương d là \(\overrightarrow{u}=(2;-1;2)\) và phương trình tham số của \(d: \left\{\begin{matrix} x=1+2t\\ y=3-t\\ z=-2+2t \end{matrix}\right.(t\in R)\Rightarrow K(1+2t;3-t;-2+3t),\)vì \(K\in d\)
+ Mặt khác \(K(1+2t; 3 -t; -2 + 2t) \in (P)\)
\(\Leftrightarrow 2(1+2t)-(3-t)+2(-2+2t)-1=0\Leftrightarrow 9t-6=0\)
\(\Leftrightarrow t=\frac{2}{3}\) suy ra \(K(\frac{7}{3};\frac{7}{3};-\frac{2}{3})\) -
-
Câu 9:
Cho tập hợp E = {1;2;3;4;5;6} và M là tập tất cả các số gồm hai chữ số phân biệt thuộc E. Lấy ngẫu nhiên một số thuộc M. Tính xác suất để tổng hai chữ số của số đó lớn hơn 7.
-
+ Số phần tử của tập M là

+ Các số có tổng hai chữ số lớn hơn 7 gồm: 26, 62, 35, 53, 36, 63, 45, 54, 46, 64, 56, 65. Có số
số
Suy ra xác suất cần tìm là

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=
Lời giải:+ Số phần tử của tập M là \(A_{6}^{2}=30\)
+ Các số có tổng hai chữ số lớn hơn 7 gồm: 26, 62, 35, 53, 36, 63, 45, 54, 46, 64, 56, 65. Có 12 số
Suy ra xác suất cần tìm là \(p=\frac{12}{30}=\frac{2}{5}\) -
-
Câu 10:
Cho a, b, c là ba số thực dương và thỏa mãn điều kiện \(\small 3(a^2+b^2+c^2)=1\) . Tìm giá trị nhỏ nhất của biểu thức
\(\small Q=\sqrt{a^2+b^2+\frac{1}{b^2}+\frac{1}{c^2}}+\sqrt{b^2+c^2+\frac{1}{c^2}+\frac{1}{a^2}}+\sqrt{c^2+a^2+\frac{1}{a^2}+\frac{1}{b^2}}\)
-
+ Ta có
suy ra
+ Sử dụng bất đẳng thức Cauchy – Schwarz, ta có:
+ Xét các véc tơ:
Ta có

và
Khi đó
+ Đặt
Xét hàmvới
. Ta có

Suy ra f(t) là hàm nghịch biến trên

hay
Dấu đẳng thức xảy ra. Vậy
khi

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:+ Ta có \((a+b+c)^2\leq 3(a^2+b^2+c^2)=1\) suy ra \(a+b+c\leq 1\)
+ Sử dụng bất đẳng thức Cauchy – Schwarz, ta có:
\(\small \sqrt{2}Q=\sqrt{2(a^2+b^2)+2(\frac{1}{b^2}+\frac{1}{c^2})}+\sqrt{2(b^2+c^2)+2(\frac{1}{c^2}+\frac{1}{a^2})}+\sqrt{2(c^2+a^2)+2(\frac{1}{a^2}+\frac{1}{b^2})}\)
\(\small \geq \sqrt{(a+b)^2+(\frac{1}{b}+\frac{1}{c})^2}+\sqrt{(b+c)^2+(\frac{1}{c}+\frac{1}{a})^2}+\sqrt{(c+a)^2+(\frac{1}{a}+\frac{1}{b})^2}\)
+ Xét các véc tơ: \(\small \vec{x}=\left ( a+b;\frac{1}{b} +\frac{1}{c}\right );\vec{y}=\left ( b+c;\frac{1}{a} +\frac{1}{c}\right );\vec{z}=\left ( c+a;\frac{1}{a} +\frac{1}{b}\right )\)
Ta có \(\small \vec{x}+\vec{y}+\vec{z}=(2(a+b+c);2\left ( \frac{1}{a}+\frac{1}{b} +\frac{1}{c} \right ))\) và \(\small \left | \vec{x} \right |+\left | \vec{y} \right |+\left | \vec{z} \right |\geq \left | \vec{x}+\vec{y}+\vec{z} \right |\)
Khi đó \(\small \sqrt{2}Q\geq \sqrt{4(a+b+c)^2+4\left ( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )^2}\geq 2\sqrt{(a+b+c)^2+\frac{81}{(a+b+c)^2}}\)
+ Đặt \(\small t=(a+b+c)^2\Rightarrow 0< t\leq 1\)
Xét hàm \(\small f(t)=t+\frac{81}{t}\) với \(\small t\in (0;1 ]\). Ta có \(\small f'(t)=1-\frac{81}{t^2}< 0,\forall t\in (0;1]\)
Suy ra f(t) là hàm nghịch biến trên \(\small (0;1]\Rightarrow f'(t)\geq f(1)=82\)
\(\small \Rightarrow \sqrt{2}Q\geq 2\sqrt{82}\) hay \(\small Q\geq 2\sqrt{41}\)
Dấu đẳng thức xảy ra \(\small \Leftrightarrow a=b=c=\frac{1}{3}\). Vậy \(\small min Q=2\sqrt{41}\) khi \(\small a =b = c = \frac{1}{3}\) -





