Đề thi thử THPT Quốc gia năm 2015 môn Toán - Sở GD&ĐT Lâm Đồng

1)
+ Tập xác định: D = R.
+ Sự biến thiên
Đạo hàm \(y' = 3x^2 - 12x + 9.\)
\(y'=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=1\\ x=3 \end{matrix}\)
- Giới hạn \(\lim_{x\rightarrow -\infty }y=-\infty ;\lim_{x\rightarrow +\infty }y=+\infty\)
- Bảng biến thiên.
- Hàm số nghịch biến trên khoảng (1;3); Hàm số đồng biến trên khoảng \((-\infty ;1)\) và khoảng \((3; +\infty ).\)
- Hàm số đạt cực đại tại điểm x = 1, y_CĐ = 0. Hàm số đạt cực tiểu tại điểm x = 3, y_CT = -4.
+ Đồ thị.
2)
+ Gọi d là tiếp tuyến của (C) tại M(x₀;y₀) và d song song với đường thẳng y = 9x – 4. Suy ra d có hệ số góc bằng 9.
+ Giải Pt: y’(x₀) = 9 ⇔ x₀ = 0 hoặc x₀ = 4. Suy ra M(0;-4); M(4; 0)
+ Tại M(0; -4), d: y = 9x – 4 (loại)
+ Tại M(4; 0), d: y = 9x - 36
Kết luận: pttt d: y = 9x - 36

1)
+ Điều kiện: \(-2< x\neq 0\)
+ Trong điều kiện đó phương trình trở thành
\(log_2x^2-log_2(x+2)-1=0\Leftrightarrow log_2x^2=log_2(x+2)+1\)
\(\Leftrightarrow log_2x^2=log_22(x+2)\)

\(\Leftrightarrow x^2=2(x+2)\Leftrightarrow \bigg \lbrack \begin{matrix} x=1+\sqrt{5}\\ x=1-\sqrt{5} \end{matrix}\)
Kết luận: nghiệm phương trình: \(x=1\pm \sqrt{5}\)
2)
+ Biến đổi phương trình về dạng:
\(1-2sin\frac{x}{2}cos\frac{x}{2}=1-sin2x\Leftrightarrow sin2x=sinx\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} 2x=x+k2\pi \\ 2x=\pi -x+k2\pi \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix} x=k2\pi \\ x=\frac{\pi }{3}+\frac{k2\pi }{3} \end{matrix}\)

Tách \(I=I_1+I_2\)
+ Tính \(I_1=\int_{1}^{2}xlnxdx\)
+ Đặt \(\left\{\begin{matrix} u=lnx\\ xdx=dv \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{1}{x}dx\\ v=\frac{x^2}{2} \end{matrix}\right.\)
+ \(I_1=\frac{x^2}{2}lnx |_{1}^{2}-\int_{1}^{2}\frac{x^2}{2}dx=2ln2-\frac{x^2}{4}|_{1}^{2}=2ln2-\frac{3}{4}\)
+ Tính \(I_2=\int_{1}^{2}\frac{x}{1+x^2}dx\)
+ Đặt \(t=1+x^2\Rightarrow dt=2xdx\Rightarrow xdx=\frac{dt}{2}\)
+ Đổi cận: \(x=1\Rightarrow t=2;x=2\Rightarrow t=5\)
+ \(I_2=\frac{1}{2}\int_{2}^{5}\frac{1}{t}dt=\frac{1}{2}ln\left | t \right ||_{2}^{5}=\frac{1}{2}ln\frac{5}{2}\)
Kết luận: \(I=2ln2-\frac{3}{4}+\frac{1}{2}ln\frac{5}{2}\)

\(\small \left\{\begin{matrix} x^2+6y-4=\sqrt{2(1-y)(x^3+1)}\\ (3-x)\sqrt{2-x}-2y\sqrt{2y-1}=0 \end{matrix}\right.\)
+ ĐK: \(\left\{\begin{matrix} x\leq 2\\ y\geq \frac{1}{2}\\ (1-y)(x^3+1)\geq 0 \end{matrix}\right.\)
 

+ Ta có: \((3-x)\sqrt{2-x}-2y\sqrt{2y-1}=0\Leftrightarrow \left [ 1+(2-x) \right ]\sqrt{2-x}=\left [ 1+(2y-1) \right ]\sqrt{2y-1}\)
+ Xét hàm số \(f(t)=(1+t^2)t=t^3+t\)
\(f'(t)=3t^2+1> 0\forall t\in R\). Hàm số tăng trên R.
+ Mà \(f(\sqrt{2-x})=f(\sqrt{2y-1})\Leftrightarrow \sqrt{2-x}=\sqrt{2y-1}\)
\(\Leftrightarrow 2-x=2y-1\Leftrightarrow 2y=3-x\)
+Với 2y = 3 – x, thay vào phương trình (1) ta có:
\(x^2+6y-4=\sqrt{2(1-y)(x^3+1)}\Leftrightarrow x^2+3(3-x)-4=\sqrt{(2(3-x))(x^3+1)}\)
\(\Leftrightarrow x^2-3x+5=\sqrt{(x-1)(x^3+1)}\)
\(\Leftrightarrow 3(x^2-x+1)-2(x^2-1)=\sqrt{(x^2-1)(x^2-x+1)}\)
\(\Leftrightarrow 3-\frac{2(x^2-1)}{x^2-x+1}=\sqrt{\frac{x^2-1}{x^2-x+1}}\)
\(\Leftrightarrow x=2\)
+ So ĐK, kết luận nghiệm của hệ phương trình: \(\left\{\begin{matrix} x=2\\ y=\frac{1}{2} \end{matrix}\right.\)

1)
+ Biến đổi đẳng thức về được \(z=-\frac{1}{2}i\)
+ Kết luận: Phần thực là 0; phần ảo là \(-\frac{1}{2}\)
2)
+ Tính được \(n(\Omega )=C_{16}^{4}\)
+ Gọi A là biến cố cần tính xác suất
+ Tính \(n(A )=C_{7}^{2}.4.5+7.C_{4}^{2}.5+7.4.C_{5}^{2}\)
+ Tính \(P(A)=\frac{n(A)}{n(\Omega )}=\frac{C_{7}^{2}.4.5+7.C_{4}^{2}.5+7.4.C_{5}^{2}}{C_{16}^{4}}=\frac{1}{2}\)

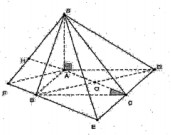
* V_S.ABCD = ?
+ Tính \(AC=2AO=2R=\frac{2a\sqrt{3}}{3}\). Suy ra \(BC=AC.cos30^0=a\)
\(AB=AC.sin30^0=\frac{a\sqrt{3}}{3}\)
+ \(S_{ABCD}=AB.BC=\frac{a^2\sqrt{3}}{3}\). Suy ra \(V_{S.ABCD}=\frac{1}{3}.S_{ABCD}.SA=\frac{a^3}{3}\)
* d(AC;SB) = ?
+ Gọi E là giao điểm của đường thẳng CD và đường thẳng đi qua B và song song với AC. Khi đó AC // (SBE).
Vậy d(AC; SB)= d(AC;(SBE)) = d(A; (SBE))
+ Từ A kẻ AF \(\perp\) BE. Ta có (SBE) \(\perp\) (SAF)
+ Kẻ AH ⊥ SF \(\Rightarrow\)  AH \(\perp\) (SBE). Vậy d(AC; SB) = d(A; (SBE)) = AH
+ Tính được \(AH=\frac{a\sqrt{39}}{13}\)

+ Phương trình đường thẳng (AD): x + y – 3 = 0
+ \(AB=2MI=3\sqrt{2}\). Từ \(S_{ABCD}=12\Rightarrow MA=MD=\sqrt{12}\)
+ Phương trình đường tròn tâm M bán kính \(R=\sqrt{2}\)  là  \((x-3)^2+y^2=2\)
+ Tọa độ điểm A, D là nghiệm của hệ phương trình:
\(\left\{\begin{matrix} x+y-3=0\\ (x-3)^2+y^2=2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=2\\ y=1 \end{matrix}\right.\vee \left\{\begin{matrix} x=4\\ y=-1 \end{matrix}\right.\)
Vậy A(2; 1), D(4; -1). Suy ra C(7;2), B(5;4)

+ Tính \(\overrightarrow{BC}(-1;1;-1)\)
+ Phương trình (P) đi qua A và có VTPT \(\overrightarrow{BC}(-1;1;-1)\) có phương trình là: x – y + z + 5 = 0
+ PT \((BC)\left\{\begin{matrix} x=1-t\\ y=5+t,t\in R\\ z=2-t \end{matrix}\right.\)
+Gọi H = (BC) ∩ (P). Suy ra tọa độ của H là nghiệm của hệ phương trình: \(\left\{\begin{matrix} x=1-t\\ y=5+t\\ z=2-t\\ x-y+z+5=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} t=1\\ x=0\\ y=6\\ z=1 \end{matrix}\right.\)
Vậy H(0;6;1). Do I đối xứng với A qua BC nên H là trung điểm của AI. Suy ra I (-1;11;7)
+ Gọi (S) là mặt cầu tâm I và tiếp xúc với (Q). Suy ra bán kính mặt cầu là \(R=d(I;(Q))=2\sqrt{6}\)
\((S): (x+1)^2+(y-11)^2+(z-7)^2=24\)
 

+ Áp dụng bất đẳng thức Cauchy ta có:
\(\frac{1}{\sqrt{a^2+ab}}+\frac{1}{\sqrt{b^2+ab}}\geq \frac{2}{\sqrt[4]{(a^2+ab)(b^2+ab)}}\geq \frac{2}{\sqrt{\frac{a^2+ab+b^2+ab}{2}}}\geq \frac{2}{\sqrt{a^2+b^2}}\)
Đẳng thức xảy ra khi và chỉ khi a = b
\(P\geq \frac{2}{\sqrt{a^2+b^2}}+\frac{2\sqrt{3}}{c+1}=\frac{2}{\sqrt{1-c^2}}+\frac{2\sqrt{3}}{c+1}\)
+ Xét hàm \(f(c)=\frac{2}{\sqrt{1-c^2}}+\frac{2\sqrt{3}}{c+1};c\in (0;1)\)
Ta có \(f'(c)=\frac{2}{(1-c^2)\sqrt{1-c^2}}-\frac{2\sqrt{3}}{(1+c^2)}=\frac{2c(1+c)^2-2\sqrt{3}(1-c^2)\sqrt{1-c^2}}{(1+c)^2(1-c)^2\sqrt{1-c^2}}\)
\(f'(c)=0\Leftrightarrow 2c(1+c)^2-2\sqrt{3}(1-c^2)\sqrt{1-c^2}=0, c\in (0;1)\)
\(\Leftrightarrow \left\{\begin{matrix} 4c^3-8c^2+9c-3=0\\ c\in (0;1) \end{matrix}\right.\Leftrightarrow c=\frac{1}{2}\)
+ Lập bảng biến thiên của hàm f(c) trên (0;1). Tìm được
\(MinP=\frac{8\sqrt{3}}{3}\)xảy ra khi  \(a=b=\frac{\sqrt{6}}{4};c=\frac{1}{2}\)