Câu hỏi trắc nghiệm (9 câu):
-
Câu 1:
Cho hàm số \(y=f(x)=-x^3+6x^2-9x+2\) có đồ thị là (C)
a, Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b, Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ thỏa mãn f''(x) = 18.-
a.
* Tập xác định D = R
*
* Giới hạn:

* Bảng biến thiên:
.jpg)
* Kết luận:
- Hàm số nghịch biến trên các khoảng

và ( ) đồng biến trên khoảng (1;3).
- Hàm số đạt cực đại tại x = 3, yCĐ = 2; đạt cực tiểu tại x = 1, yCT = -2.
* Đồ thị:
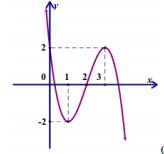
b)
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ thỏa mãn
f''(x) =
Ta có

Theo giả thiết thì


Vậy phương trình tiếp tuyến là:

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấu
được ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
* Tập xác định D = R
* \(y'=-3x^2+12x-9x,y'=0\Leftrightarrow\bigg \lbrack \begin{matrix} x=1\\ x=3 \end{matrix}\)
* Giới hạn: \(\lim_{x\rightarrow +\infty }y=-\infty , \lim_{x\rightarrow -\infty }y=+\infty\)
* Bảng biến thiên:
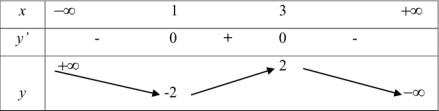
* Kết luận:
- Hàm số nghịch biến trên các khoảng \((-\infty ;1), (3;+\infty )\)và ( ) đồng biến trên khoảng (1;3).
- Hàm số đạt cực đại tại x = 3, yCĐ = 2; đạt cực tiểu tại x = 1, yCT = -2.
* Đồ thị:

b)
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ thỏa mãn
f''(x) = 18
Ta có \(f''(x)=-3x^2+12x-9\Rightarrow f''(x)=-6x+12\)
Theo giả thiết thì \(f''(x)=18\Leftrightarrow x=-1\Rightarrow y=18\)
\(f'(x)=-3x^2+12x-9\Rightarrow f'(-1)=-24\)
Vậy phương trình tiếp tuyến là: \(y = -24(x+1)+18 \ \ hay \ \ y = -24x-6\) -
-
Câu 2:
a. Cho \(cosx=-\frac{3}{5},(\pi < x< \frac{3\pi }{2})\). Tính giá trị của \(sin(x-\frac{\pi }{6})\)
b. Giải phương trình \(4^{x^2-2x}+3.2^{x^2-2x}-4=0 \ \ \ (x\in R)\)-
a) Ta có:

 . Vì
. Vì nên

khi đó:

b)
Phương trìnhcó thể viết lại là:
Đặt
Phương trình (*) trở thành
.jpg)
So với điều kiện thì t =
 thỏa, khi đó
thỏa, khi đó 
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a) Ta có: \(sin^2=1-cos^x=1-\frac{9}{25}=\frac{16}{25}\) . Vì \(\left ( \pi < x< \frac{3\pi }{2} \right )\) nên \(sinx=-\frac{4}{5}\)
khi đó: \(sin\left ( x-\frac{\pi }{6} \right )=sinx.cos\left ( \frac{\pi }{6} \right )-sin\left ( \frac{\pi }{6} \right )cosx\)
\(=-\frac{4}{5}.\frac{\sqrt{3}}{2}+\frac{1}{2}.\frac{3}{5}=\frac{3-4\sqrt{3}}{10}\)
b)
Phương trình \(4^{x^2-2x}+3.2^{x^2-2x}-4=0 (*)\) có thể viết lại là:
\(2^{2(x^2-2x)}+3.2^{x^2-2x}-4=0\)
Đặt \(t=2^ {(x^2-2x)} \ \(t>0)\)
Phương trình (*) trở thành \(t^2+3t-4=0\Leftrightarrow \bigg \lbrack\begin{matrix} t=1\\ t=-4 \end{matrix}\)
So với điều kiện thì t = 1 thỏa, khi đó \(2^ {(x^2-2x)}=1\)
\(\Leftrightarrow x^2-2x=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=0\\ x=2 \end{matrix}\) -
-
Câu 3:
a, Tìm môđun của số phức, biết rằng \((1-2i)z-\frac{9+7i}{3-i}=5-2i\)
b,Tìm hệ số của số hạng chứa \(x^4\) trong khai triển nhị thức Niu-tơn của \(\left ( x^2-\frac{2}{\sqrt[3]{x^2}} \right )^{10}\) với x > 0
-
a) Ta có




b) Số hạng tổng quát có dạng là
Theo giả thiết, số hạng tổng quát chứa x4 khi và chỉ khi


Vậy hệ số của số hạng chứa x4 là:


Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a) Ta có \((1-2i)z-\frac{9-7i}{3-i}=5-2i\Leftrightarrow (1-2i)z=7+i\)
\(\Leftrightarrow z= \frac{7+i}{1-2i}=1+3i\Rightarrow \left | z \right |=\sqrt{10}\)
b) Số hạng tổng quát có dạng là \(C_{10}^{k}(x^2)^{10-k}\left ( \frac{-2}{\sqrt[3]{x^2}} \right )=C_{10}^{k}x^{20-\frac{8}{3}k}.(-2)^k\) \((0\leq k\leq 10)\)
Theo giả thiết, số hạng tổng quát chứa x4 khi và chỉ khi \(20-\frac{8}{3}k=4\Leftrightarrow k=6\)
Vậy hệ số của số hạng chứa x4 là: \(a=C_{10}^{6}(-2)^6=13440\) -
-
Câu 4:
Tính tích phân \(I=\int_{1}^{e}\left ( \frac{2x+lnx+1}{x} \right )dx\)
-

đặt




Vậy



Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(I=\int_{1}^{e}2dx+\int_{1}^{e}\frac{lnx+1}{x}\)
\(I_{1}=\int_{1}^{e}2dx=(2x)|_{1}^{e}=2e-2\)
\(I_{2}=\int_{1}^{e}\frac{lnx+1}{x}dx\) đặt \(t=lnx+1\Rightarrow dt=\frac{1}{x}dx\)
\(x=1\Rightarrow t=1;x=e\Rightarrow t=2\)
\(I_2=\int_{1}^{2}tdt=\frac{t^2}{2} |_{1}^{2}=\frac{3}{2}\)Vậy \(I=2e-2+\frac{3}{2}=2e-\frac{1}{2}\)
-
-
Câu 5:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A , BC = 2a, AB = a và mặt bên BB'C'C là hình vuông. Tính theo a thể tích của khối lăng trụ và khoảng cách giữa hai đường thẳng AA'BC'.
-
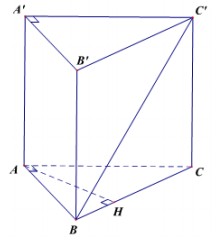
Ta có tam giác ABC vuông tại A nên

.jpg)
Vì BB'C'C là hình vuông nên BB '= BC = a
a
Vậy.jpg)


(đvtt)
Vì AA' // BB' nên AA' // (BB'C'C). Do đó d(AA',BC) = d(AA',(BB'C'C)) = d(A,(BB'C'C))"
Dựng(H thuộc BC). Khi đó
và
Suy ra. Suy ra
Xét tam giác vuông ABC, ta có.jpg)
Vậy.jpg)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:

Ta có tam giác ABC vuông tại A nên \(AC=\sqrt{BC^2+AB^2}=a\sqrt{3}\)
\(S_{ABC}=\frac{1}{2}AB.AC=\frac{a^2\sqrt{3}}{2}\)
Vì BB'C'C là hình vuông nên BB '= BC = 2a
Vậy \(V_{ABC.A'B'C'}=S_{ABC}.BB'=\frac{a^2\sqrt{3}}{2}2a=a^2\sqrt{3}\) (đvtt)
Vì AA' // BB' nên AA' // (BB'C'C). Do đó d(AA',BC) = d(AA',(BB'C'C)) = d(A,(BB'C'C))"
Dựng \(AH\perp BC\) (H thuộc BC). Khi đó \(AH\perp BC\) và \(AH\perp BB'\)
Suy ra \(AH\perp (BB'C'C)\). Suy ra \(d(A,(BB'C'C))=AH\)
Xét tam giác vuông ABC , ta có \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{a\sqrt{3}}{2}\)
Vậy \(d(AA',BC')=\frac{a\sqrt{3}}{2}\) -
-
Câu 6:
Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD. Biết điểm A có tung độ dương , đường thẳng AB có phương trình 3x + 4y -18 = 0 , điểm \(M\left ( \frac{21}{4};-1 \right )\) thuộc cạnh BC, đường thẳng AM cắt đường thẳng CD tại N thỏa mãn BM.DN = 25. Tìm tọa độ các đỉnh của hình vuông ABCD.
-
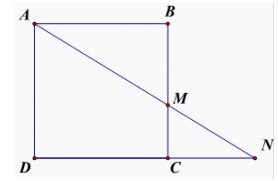
Đường thẳng BC qua M và vuông góc với AB nên:
BC: 4x - 3y - 24 = 0. Khi đó, tọa độ B là nghiệm của hệ:
Ta thấy các tam giác sau đồng dạng với nhau
Suy ra
Suy ra 25 = AB2 hay cạnh của hình vuông bằng 5.
Gọi, khi đó
.jpg)
Vì điểm A có tung độ dương nên A(2;3)
Phương trình đường thẳng CD có dạng
Vì cạnh hình vuông bằng 5 nên.jpg)
* Với m = 7, pt CD: 3x + 4y + 7 = 0, khi đó tọa độ C là nghiệm của hệ
.jpg) (thoả vì MC < 5)
(thoả vì MC < 5)
Suy ra tọa độ D(-1;-1)
* Với m = -43 , pt CD: 3x + 4y - 43 = 0, khi đó tọa độ C là nghiệm của hệ
.jpg) (không thỏa vì MC < 5)
(không thỏa vì MC < 5)Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Đường thẳng BC qua M và vuông góc với AB nên:
BC: 4x - 3y - 24 = 0. Khi đó, tọa độ B là nghiệm của hệ:
\(\left\{\begin{matrix} 4x-3y-24=0\\ 3x+4y-18=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=6\\ y=0 \end{matrix}\right.\Rightarrow B(6;0)\)
Ta thấy các tam giác sau đồng dạng với nhau \(\Delta MBA\sim \Delta MCN\sim \Delta ADN\)
Suy ra \(\frac{MB}{AB}=\frac{MC}{NC}=\frac{AD}{ND}\Rightarrow MB.ND=AB.AD\)
Suy ra 25 = AB2 hay cạnh của hình vuông bằng 5.
Gọi \(A(4a+6;-3a)\in AB\), khi đó \(25=AB^2\Leftrightarrow 16a^2+9a^2=25\Leftrightarrow \bigg \lbrack \begin{matrix} a=1\\ a=-1 \end{matrix}\)
Vì điểm A có tung độ dương nên A(2;3)
Phương trình đường thẳng CD có dạng \(3x + 4y + m = 0 (m\neq -18)\)
Vì cạnh hình vuông bằng 5 nên \(d(B,CD)=\frac{\left | 18+m \right |}{5}=5\Leftrightarrow \bigg \lbrack\begin{matrix} m=7\\ m=-43 \end{matrix}\)
* Với m = 7 , pt CD: 3x + 4y + 7 = 0, khi đó tọa độ C là nghiệm của hệ
\(\left\{\begin{matrix} 4x-3y-24=0\\ 3x+4y+7=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=3\\ y=-4 \end{matrix}\right.\Rightarrow C(3;-4)\) (thoản vì MC < 5)
Suy ra tọa độ D(-1;-1)
* Với m = -43 , pt CD: 3x + 4y - 43 = 0, khi đó tọa độ C là nghiệm của hệ
\(\left\{\begin{matrix} 4x-3y-24=0\\ 3x+4y-43=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=9\\ y=4 \end{matrix}\right.\Rightarrow C(9;4)\)(không thỏa vì MC < 5) -
-
Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho điểm A(2;-2;1) đường thẳng \(d: \frac{x-1}{1}=\frac{y-2}{2}=\frac{z+1}{1}\)và mặt phẳng (P): x - 2y - z - 3 = 0. Viết phương trình mặt phẳng qua điểm A, song song với đường thẳng d và vuông góc với mặt phẳng (P).
-
Ta có:

là VTCP của đường thẳng d.

là VTPT của mặt phẳng (P)
Gọi (Q) là mặt phẳng cần tìm theo giả thiết thì


là VTPT của mặt phẳng (Q).
Phương trình mp (Q):


Hay:


Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có: \(\overrightarrow{u_d}=(1;2;1)\) là VTCP của đường thẳng d.
\(\overrightarrow{u_{(P)}}=(1;-2;-1)\) là VTPT của mặt phẳng (P)
Gọi (Q) là mặt phẳng cần tìm theo giả thiết thì \(\left [ \overrightarrow{u_d},\overrightarrow{u_{(P)}} \right ]=(0;-2;4)\) là VTPT của mặt phẳng (Q).
Phương trình mp (Q): \(0(x-2)-2(y+2)+4(z-1)=0\)
Hay: \(y-2z+4=0\) -
-
Câu 8:
Giải bất phương trình \(\sqrt{4x^2+3}+6x-1\geq \sqrt{4x^2+15} \ \ (x\in R)\)
-
ĐK:
. Với điều kiện này thì bất phương trình đã cho tương đương:


Ta có:


Vì
nên
Do đó
Khi đó



Kết hợp với điều kiện, nghiệm của bất phương trình là

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:ĐK: \(x\in R\). Với điều kiện này thì bất phương trình đã cho tương đương:
\(\sqrt{4x^2+3}-2+6x-3+4-\sqrt{4x^2+15}\geq 0\)
\(\Leftrightarrow \frac{4x^2-1}{\sqrt{4x^2+3}+2}+3(2x-1)+\frac{1-4x^2}{4+\sqrt{4x^2+15}}\geq 0\)
\(\Leftrightarrow (2x-1)\left ( \frac{2x+1}{\sqrt{4x^2+3}+2}+3-\frac{2x+1}{4+\sqrt{4x^2+15}} \right )\geq 0\)
Ta có:
\(\sqrt{4x^2+3}+6x-1\geq \sqrt{4x^2+15}\Leftrightarrow 6x-1\geq \sqrt{4x^2+15}-\sqrt{4x^2+3}>0\)
\(\Rightarrow x> \frac{1}{6}\Rightarrow 2x+1> 0\)
Vì \(\sqrt{4x^2+3}+2< 4+\sqrt{4x^2+15}\) nên \(\frac{2x+1}{\sqrt{4x^2+3}+2}-\frac{2x+1}{4+\sqrt{4x^2+15}}> 0\)
Do đó \(\frac{2x+1}{\sqrt{4x^2+3}+2}+3-\frac{2x+1}{4+\sqrt{4x^2+15}}> 0\)
Khi đó \((2x-1)\left ( \frac{2x+1}{\sqrt{4x^2+3}+2}+3-\frac{2x+1}{4+\sqrt{4x^2+15}} \right )\geq 0\)
\(\Leftrightarrow 2x-1\geq 0\Leftrightarrow x\geq \frac{1}{2}\)
Kết hợp với điều kiện , nghiệm của bất phương trình là \(x\geq \frac{1}{2}\) -
-
Câu 9:
Cho các số thực không âm x, y, z thỏa mãn \(x\geq y\geq z\) và x2 + y2 + z2 = 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(A=2xy+8yz+5zx+\frac{10}{x+y+z}\)
-
Ta có:
Đặt t = x + y + z


Và
Xét hàm số:
trên
luôn đồng biến trên D
dấu đẳng thức xảy ra khi và chỉ khi
Giá trị nhỏ nhất của A là
, đạt được khi y = z =
 ,
, Xét hàm số:
trên

luôn đồng biến trên D


Vậy giá trị lớn nhất của A là
 , đạt được khi x = y = z =
, đạt được khi x = y = z = 
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có: \(A=(x+y+z)^2-3+3xz+6yz+\frac{10}{x+y+z}\)
\(0\leq 3xz+6yz=3z(x+2y)\leq \left ( \frac{3z+x+2y}{2} \right )^2\leq (x+y+z)^2\)
\((x+y+z)^2-3+\frac{10}{x+y+z}\leq A\leq 2(x+y+z)^2-3+\frac{10}{x+y+z}\)
Đặt t = x + y + z
\(\Rightarrow 3=x^2+y^3+z^2\leq (x+y+z)^2\leq 3(x^2+y^3+z^2)=9\)
\(\Rightarrow \sqrt{3}\leq t\leq 3\)
Và \(t^2-3+\frac{10}{t}\leq A\leq 2t^2-3+\frac{10}{t}\)
Xét hàm số: \(f(t)=t^2+\frac{10}{t}-3\) trên \(D=\left [ \sqrt{3};3 \right ],f'(t)=2t-\frac{10}{t^2}=\frac{2t^3-10}{t^2}>0,\forall t\in D\)
\(\Rightarrow f(t)\) luôn đồng biến trên D \(\Rightarrow A\geq min_D \ f(t)=f(\sqrt{3})=\frac{10}{\sqrt{3}}\) dấu đẳng thức xảy ra khi và chỉ khi \(\left\{\begin{matrix} z(x+2y)=0\\ x+y+z=\sqrt{3}\\ x^2+y^2+z^2=3 \end{matrix}\right.\)
\(\Leftrightarrow y=z=0,x=\sqrt{3}(x\geq y\geq z)\)
Giá trị nhỏ nhất của A là \(\frac{10}{\sqrt{3}}\), đạt được khi y = z = 0, \(x=\sqrt{3}\)
Xét hàm số: \(g(t)=2t^2+\frac{10}{t}-3\) trên \(D=\left [ \sqrt{3};3 \right ], g'(t)=4t-\frac{10}{t^2}\) \(=\frac{4t^3-10}{t^2}>0\) \(\forall t\in D\)
\(\Rightarrow g(t)\) luôn đồng biến trên D \(\Rightarrow A\leq min_D \ g(t)=g(3)=\frac{55}{3}\)
\(\left\{\begin{matrix} 3z=x+2y\\ x+y+z=3\\ x^2+y^3+z^2=3 \end{matrix}\right.\Leftrightarrow x=y=z=1\)
Vậy giá trị lớn nhất của A là \(\frac{55}{3}\), đạt được khi x = y = z = 1 -





