Câu hỏi trắc nghiệm (9 câu):
-
Câu 1:
Cho hàm số \(y=x^3-3x^2+2\)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
2) Tìm các giá trị của m để phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt, trong đó có đúng 2 nghiệm lớn hơn 1.-
1.Học sinh tự giải
2.
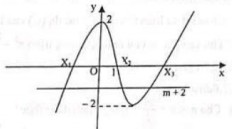
Từ ý 1) ta thấy đồ thị của hàm số y = x3 – 3x2 + 2 cắt trục hoành tại 3 điểm phân biệt có hoành độ x1, x2 = 1, x3 với x1x2= 1 < x3.
 -
-
Từ đó suy ra phương trình


Có ba nghiệm phân biệt, trong đó có đúng 2 nghiệm lớn hơn 1 khi và chỉ khi đường thẳng y = m + cắt đồ thị (C) tại 3 điểm phân biệt trong đó có đúng hai nghiệm có hoành độ lớn hơn 1.
cắt đồ thị (C) tại 3 điểm phân biệt trong đó có đúng hai nghiệm có hoành độ lớn hơn 1.
Từ đồ thị (C) suy ra điều kiện là:



Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:1.Học sinh tự giải
2.
Từ ý 1) ta thấy đồ thị của hàm số y = x3 – 3x2 + 2 cắt trục hoành tại 3 điểm phân biệt có hoành độ x1, x2 = 1, x3 với x1x2= 1 < x3.

Từ đó suy ra phương trình \(x^3-3x^2-m=0\Leftrightarrow x^3-3x^2+2=m+2\)
Có ba nghiệm phân biệt, trong đó có đúng 2 nghiệm lớn hơn 1 khi và chỉ khi đường thẳng y = m + 2 cắt đồ thị (C) tại 3 điểm phân biệt trong đó có đúng hai nghiệm có hoành độ lớn hơn 1.
Từ đồ thị (C) suy ra điều kiện là: \(-2< m+2< 0\Leftrightarrow -4< m< -2\)
-
-
Câu 2:
1) Cho \(\pi < \alpha < \frac{3\pi }{2}\). Chứng minh đẳng thức: \(\frac{\sqrt{1+cos\alpha }+\sqrt{1-cos\alpha }}{\sqrt{1+cos\alpha }-\sqrt{1-cos\alpha }}=cot(\frac{\alpha }{2}+\frac{\pi }{4})\)
2) Giải phương trình: \(4^{x^2+x}+2^{1-x^2}=2(x+1)^2+1\)-
1. Ta có
Vìnên
 và
và  , suy ra
, suy ra

=
(đpcm)
2. PT
 =0
=0



Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có \(\frac{\sqrt{1+cos\alpha}+\sqrt{1-cos\alpha}}{\sqrt{1+cos\alpha}-\sqrt{1-cos\alpha}}=\) \(\frac{\sqrt{1+cos\alpha}+\sqrt{1-cos\alpha}}{\sqrt{1+cos\alpha}-\sqrt{1-cos\alpha}}=\frac{\sqrt{2cos^2\frac{\pi }{2}}+\sqrt{2sin^2\frac{\pi }{2}}}{\sqrt{2cos^2\frac{\pi }{2}}-\sqrt{2sin^2\frac{\pi }{2}}}\) \(=\frac{\left | cos\frac{\pi }{2} \right |+\left | sin\frac{\pi }{2} \right |}{\left | cos\frac{\pi }{2} \right |+\left | sin\frac{\pi }{2} \right |}\)
Vì \(\pi < \alpha < \frac{3\pi }{2}\) nên \(cos\frac{\alpha }{2}< 0\) và \(sin\frac{\alpha }{2}> 0\), suy ra
\(\frac{\sqrt{1+cos\alpha}+\sqrt{1-cos\alpha}}{\sqrt{1+cos\alpha}-\sqrt{1-cos\alpha}}=\frac{sin\frac{\alpha }{2}-cos\frac{\alpha }{2}}{-sin\frac{\alpha }{2}-cos\frac{\alpha }{2}}=\frac{cos(\frac{\alpha }{2}+\frac{\alpha }{4})}{sin(\frac{\alpha }{2}+\frac{\alpha }{4})}\)
= \(cot(\frac{\alpha }{2}+\frac{\alpha }{4})\) (đpcm)
2. PT
\(\Leftrightarrow 2^{2x^2+2x}+2^{1-x^2}-2^{x^2+2x+1}-1=0\)
\(\Leftrightarrow -2^{2x^2+2x}(2^{1-x^2}-1)+(2^{1-x^2}-1)=0\)
\(\Leftrightarrow (2^{1-x^2}-1)+(2^{1-x^2}-1)=0\Leftrightarrow \bigg \lbrack \begin{matrix} 2^{1-x^2}=1\\ 2^{2x^2+2x}=1 \end{matrix}\Leftrightarrow \bigg \lbrack \begin{matrix} x^2=1\\ 2x^2+2x=0 \end{matrix}\)
\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=\pm 1\\ x=0 \end{matrix}\) -
-
Câu 3:
Giải phương trình \(2x^2-6x-5(x-2)\sqrt{x+1}+10=0\)
-
Điều kiện
. Phương trình đã cho tương đương với





Xét

Xét
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Điều kiện \(x \geq -1\). Phương trình đã cho tương đương với
\(-5(x-2)\sqrt{x+1}+2(x+1)+2(x^2-4x+4)=0\)
\(\Leftrightarrow 2(x-2)^2-4(x-2)\sqrt{x+1}-(x-2)\sqrt{x+1}+2(\sqrt{x+1})^2=0\)
\(\Leftrightarrow 2(x-2)\left [ (x-2)-2\sqrt{x+1} \right ]-\sqrt{x+1}\left [ (x-2)-2\sqrt{x+1} \right ]=0\)
\(\Leftrightarrow \left [ (x-2)-2\sqrt{x+1} \right ]\left [ 2(x-2)-\sqrt{x+1} \right ]=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x-2=2\sqrt{x+1}\\ 2x-4=\sqrt{x+1} \end{matrix}\)
Xét \(x-2=2\sqrt{x+1}=x-2\Leftrightarrow \left\{\begin{matrix} x\geq 2\\ x^2-8x=0 \end{matrix}\right.\Leftrightarrow x=8\)
Xét \(\sqrt{x+1}=2x-4\Leftrightarrow \left\{\begin{matrix} x\geq 2\\ 4x^2-17x+15 \end{matrix}\right.\Leftrightarrow x=3\)
Vậy nghiệm của phương trình là x = 3, x = 8. -
-
Câu 4:
Tính tích phân \(I=\int_{\frac{1}{2}}^{\frac{1}{4}}\frac{dx}{x^4(x^2-1)}\)
-
Ta có:







Vậy
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có: \(I=\int_{\frac{1}{4} }^{\frac{1}{2}}\frac{1-x^2+x^2}{x^4(x^2-1)}dx= \int_{\frac{1}{4} }^{\frac{1}{2}}\frac{dx}{x^4}+\int_{\frac{1}{4} }^{\frac{1}{2}}\frac{dx}{x^2(x^2-1)}\) \(=-\int_{\frac{1}{4} }^{\frac{1}{2}}\frac{dx}{x^4}+\int_{\frac{1}{4} }^{\frac{1}{2}}\left ( \frac{1}{x^2-1}-\frac{1}{x^2} \right )dx\)
\(=-\int_{\frac{1}{4} }^{\frac{1}{2}}\frac{dx}{x^4}+\frac{1}{2}\int_{\frac{1}{4} }^{\frac{1}{2}}\left ( \frac{1}{x^2-1}-\frac{1}{x^2} \right )dx\) \(-\int_{\frac{1}{4} }^{\frac{1}{2}}\frac{dx}{x^2}=\frac{1}{3x^3}\bigg |_{\frac{1}{4}}^{\frac{1}{2}}+\frac{1}{2}ln\frac{\left | x-1 \right |}{\left | x+1 \right |}\bigg |_{\frac{1}{4}}^{\frac{1}{2}}\) \(+\frac{1}{x}\bigg |_{\frac{1}{4}}^{\frac{1}{2}}\)
\(=\frac{1}{3}(8-64)+\frac{1}{2}(ln\frac{1}{3}-ln\frac{3}{5})+(2-4)=-\frac{62}{3}+\frac{1}{2}ln\frac{5}{9}\)
Vậy \(I=-\frac{62}{3}+\frac{1}{2}ln\frac{5}{9}\)
-
-
Câu 5:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và đường cao đều bằng a
1) Tính khoảng cách giữa hai đường thẳng AB và SC.
2) Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.-
1. Tính khoảng cách:
Gọi M, N thứ tự là trung điểm của CD, AB; H là tâm của đáy ABCD. Do AB // CD nên d(AB,SC) = d(N,(SCD))
Trong ∆SHM kẻ HE ⊥ SM, ta có
Do CDSH
HE
(SCD)
d(H, (SCD))= HE. Ta có HM = HN nên d(N,(SCD))=
 HE. Trong tam giác vuông SHM có SH. HM = HE.SM
HE. Trong tam giác vuông SHM có SH. HM = HE.SM 
Vậy
.jpg)
2. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
Hình chóp S.ABCD đều nên SH là trục của đáy ABCD. Khi đó tâm O của khối cầu ngoại tiếp hình chóp là giao điểm của mặt phẳng trung trực của một cạnh bên hình chóp và trục SH.
Trong ∆SAH vuông kẻ đường trung trực của cạnh SA, gọi O là giao điểm của đường trung trực này với SH.
Khi đó SO là bán kính của khối cầu ngoại tiếp hình chóp S.ABCD. Trong ∆SAH có
Gọi I là trung điểm của SA. Ta có

Thể tích khối cầu là

(đvtt)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:- Tính khoảng cách:
Gọi M, N thứ tự là trung điểm của CD, AB; H là tâm của đáy ABCD. Do AB // CD nên d(AB,SC) = d(N,(SCD))
Trong ∆SHM kẻ HE ⊥ SM, ta có \(SM=\sqrt{SH^2+HM^2}=\frac{a\sqrt{5}}{5}\)
Do CD \(\perp\) SH \(\Rightarrow\) HE \(\perp\) (SCD) \(\Rightarrow\) d(H, (SCD))= HE. Ta có HM = HN nên d(N,(SCD))= 2HE. Trong tam giác vuông SHM có SH. HM = HE.SM \(\Rightarrow\) \(HE = \frac{a\sqrt{5}}{5}\)
Vậy \(d(AB,SC)=\frac{2a\sqrt{5}}{5}\)
.jpg)
- Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
Hình chóp S.ABCD đều nên SH là trục của đáy ABCD. Khi đó tâm O của khối cầu ngoại tiếp hình chóp là giao điểm của mặt phẳng trung trực của một cạnh bên hình chóp và trục SH.
Trong ∆SAH vuông kẻ đường trung trực của cạnh SA, gọi O là giao điểm của đường trung trực này với SH.
Khi đó SO là bán kính của khối cầu ngoại tiếp hình chóp S.ABCD. Trong ∆SAH có \(SA=\sqrt{SH^2+HA^2}=\frac{2\sqrt{6}}{2}\)
Gọi I là trung điểm của SA. Ta có \(\Delta SHA\sim \Delta SIO \Rightarrow SO=\frac{SI.SA}{SH}=\frac{3a}{4}\)
Thể tích khối cầu là \(V=\frac{4\pi }{3}(\frac{3a}{4})^3=\frac{9\pi a^3}{16}\) (đvtt) -
-
Câu 6:
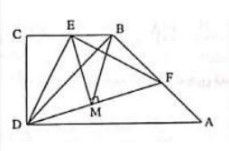
Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang vuông ABCD có \(\widehat{BCD}=\widehat{ADC}=90^0\), và BC = CD = \(\frac{1}{2}AD\). Qua điểm E thuộc cạnh BC kẻ đường thẳng vuông góc với DE cắt đường thẳng AB tại F. Tìm tọa độ các điểm B, C, D biết A(6;-2), E(1;2) và F(5;-1)
-
Từ giả thiết suy ra tam giác ABD vuông cân tại B. Gọi M là trung điểm của DF thìcân tại
và
. Xét tứ giác BEMF có

Suy ra
. Vậy ∆EDF vuông cân tại E, nên ED = EF = 5.
Từ đó xác định được D, do đó B và C cũng được xác định.
Ta có:, phương trình DE: 4x – 3y + 2 = 0.
Giả sửkhi đó ED = 5


+ Với t = 4. Khi đó D(4;6),
, phương trình BD: x – y + 2 = 0 và phương trình AF: x + y – 4 = 0.
Tọa độ điểm B là nghiệm của hệ phương trình
Mặt khác điểm B phải thuộc đường thẳng d đi qua E song song với AD, nên tọa độ điểm B phải thỏa mãn phương trình đường thẳng d: x + y – 6 = 0, khi đó: 4 + 3 – 6 = 0. Điều này mâu thuẫn.
x + y – 6 = 0, khi đó: 4 + 3 – 6 = 0. Điều này mâu thuẫn.+ Với t = -2. Khi đó D(-2;-2), phương trình BD: x – y = 0 và B là giao điểm của BD và AF. Suy ra B(2;2). Điểm B phải thuộc đường thẳng qua E song song với AD: y – 2 = 0, rõ ràng điểm B(2;2) thỏa mãn
Ta có
. Từ đó suy ra điểm C(-2;2). Khi đó
và
Vậy B(2;2), C(-2;2) và D(-2;-2)Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Từ giả thiết suy ra tam giác ABD vuông cân tại B. Gọi M là trung điểm của DF thì \(ME=\frac{DF}{2}=MB\Rightarrow \Delta MEB\) cân tại \(M\Rightarrow\widehat{MEB}=\widehat{MBE}\) và \(\widehat{MFB}=\widehat{MBF}\). Xét tứ giác BEMF có \(\widehat{MBE}+\widehat{MFB}=\widehat{MBE}+\widehat{MBF}=\widehat{EBF}=135^0\)
Suy ra \(\widehat{EMF}=360^0-2.135^0=90^0\). Vậy ∆EDF vuông cân tại E, nên ED = EF = 5.
Từ đó xác định được D, do đó B và C cũng được xác định.
Ta có: \(\overrightarrow{EF}=(4;-3)\), phương trình DE: 4x – 3y + 2 = 0.
Giả sử \(D(t;\frac{4t+2}{3})\) khi đó ED = 5 \(\Leftrightarrow (t-1)^2+(\frac{4t-4}{3})^2=25\)
\(\Leftrightarrow (t-1)^2=9\Leftrightarrow \bigg \lbrack\begin{matrix} t=-2\\ t=4 \end{matrix}\)
+ Với t = 4. Khi đó D(4;6), \(\overrightarrow{FA}=(1;-1)\), phương trình BD: x – y + 2 = 0 và phương trình AF: x + y – 4 = 0.
Tọa độ điểm B là nghiệm của hệ phương trình \(\left\{\begin{matrix} x-y+2=0\\ x+y-4=0 \end{matrix}\right.\Leftrightarrow B(1;3)\)
Mặt khác điểm B phải thuộc đường thẳng d đi qua E song song với AD, nên tọa độ điểm B phải thỏa mãn phương trình đường thẳng d: 4x + y – 6 = 0, khi đó: 4 + 3 – 6 = 0. Điều này mâu thuẫn.+ Với t = -2. Khi đó D(-2;-2), phương trình BD: x – y = 0 và B là giao điểm của BD và AF. Suy ra B(2;2). Điểm B phải thuộc đường thẳng qua E song song với AD: y – 2 = 0, rõ ràng điểm B(2;2) thỏa mãn
Ta có\(\overrightarrow{BC}=\frac{1}{2}\overrightarrow{AD}\). Từ đó suy ra điểm C(-2;2). Khi đó \(\overrightarrow{BC}.\overrightarrow{CD}=0=\overrightarrow{AD}.\overrightarrow{CD}\Leftrightarrow CD\perp BC\) và \(CD\perp AD\)
Vậy B(2;2), C(-2;2) và D(-2;-2) -
-
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x – 2y + z = 0 và đường thẳng d: \(\frac{x-1}{2}=\frac{y}{1}=\frac{z+2}{-1}\) . Gọi A là giao điểm của (P) và d. Tìm tọa độ điểm M thuộc d và khoảng cách từ M đến mặt phẳng (P), biết AM = \(\sqrt{6}\)
-
.jpg)
Gọi véc tơ pháp tuyến của mp (P) là(
 ;-2;1), véc tơ chỉ phương của đường thẳng d là
;-2;1), véc tơ chỉ phương của đường thẳng d là (2;1;
 ) và góc tạo bởi d và (P) là
) và góc tạo bởi d và (P) là .
Ta có
Giả sử M(1+2t; t; -2-t) và H là hình chiếu vuông góc của M trên (P).
Khi đó ta cóVà
Suy ra

M1 (
 ;0;-2) và M2 (
;0;-2) và M2 ( ;-2;0)
;-2;0)
Vậy có hai điểm M1( ;0;-2) và M2 (
;0;-2) và M2 ( ;-2;0) thỏa mãn AM =
;-2;0) thỏa mãn AM = và khoảng cách đến (P) bằng
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:.jpg)
Gọi véc tơ pháp tuyến của mp (P) là \(\overrightarrow{n_P}=(1;-2;1)\), véc tơ chỉ phương của đường thẳng d là \(\overrightarrow{n_d}=(2;1;-1)\) và góc tạo bởi d và (P) là \(\alpha\).
Ta có \(sin\alpha =\frac{\left | \overrightarrow{n_P}. \overrightarrow{n_d} \right |}{\left | \overrightarrow{n_P}\right |\left |\overrightarrow{n_d} \right |}=\frac{\left | 1.2-2.1-1.1 \right |}{\sqrt{6}.\sqrt{6}}=\frac{1}{6}\)
Giả sử M(1+2t; t; -2-t) và H là hình chiếu vuông góc của M trên (P).
Khi đó ta có \(MH=AM.sin\alpha =\frac{\sqrt{6}}{6}\)Và \(MH=d(M,(P))=\frac{\left | 4+2t-2t-2-t \right |}{\sqrt{6}}=\frac{\left | 1+t \right |}{\sqrt{6}}\)/
Suy ra \(\frac{\left | 1+t \right |}{\sqrt{6}}=\frac{\sqrt{6}}{6}\Leftrightarrow \left | 1+t \right |=1\Leftrightarrow \bigg \lbrack\begin{matrix} t=0\\ t=-2 \end{matrix}\Rightarrow\) M1 (1;0;-2) và M2 (-3;-2;0)
Vậy có hai điểm M1(1;0;-2) và M2 (-3;-2;0) thỏa mãn AM = \(\sqrt{6}\) và khoảng cách đến (P) bằng \(\frac{\sqrt{6}}{6}\) -
-
Câu 8:
Trong một hộp đựng các tấm bia, trên mỗi tấm bìa được ghi một số gồm 5 chữ số khác nhau được tạo thành từ 5 chữ số 1, 2, 3, 4, 5. Lấy ngẫu nhiên từ hộp ra một tấm bìa. Tìm xác suất để tấm bìa được lấy ra mà số ghi trên đó có hai chữ số 1 và 2 đứng cạnh nhau.
-
Số phần tử của không gian mẫu là N(Ω) = P5 =
 ! =
! = 
Gọi A là biến cố ứng với tấm bìa được lấy ra mà số ghi trên đó có hai chữ số 1 và 2 đứng cạnh nhau.
Trường hợp chữ số 1 đứng bên trái, chữ số 2 đứng kề bên phải. Có 4 cách chọn vị trí cho 2 chữ số 1, 2 đứng kề nhau. Với mỗi cách chọn vị trí có hai chữ số 12 thì P3 = ! =
! =  cách chọn cho 3 chữ số còn lại.
cách chọn cho 3 chữ số còn lại.
Do đó trong trường hợp này có 4. =
=  số tạo thành.
số tạo thành.
Trường hợp chữ số 2 đứng bên trái chữ số 1 đứng kề bên phải
Hoàn toàn tương tự như trên ta cũng có 24 số được tạo thành.
Suy ra N(A) = 24 + =
= 
VậyCác em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Số phần tử của không gian mẫu là N(Ω) = P5 = 5! = 120
Gọi A là biến cố ứng với tấm bìa được lấy ra mà số ghi trên đó có hai chữ số 1 và 2 đứng cạnh nhau.
Trường hợp chữ số 1 đứng bên trái, chữ số 2 đứng kề bên phải. Có 4 cách chọn vị trí cho 2 chữ số 1, 2 đứng kề nhau. Với mỗi cách chọn vị trí có hai chữ số 12 thì P3 = 3! = 6 cách chọn cho 3 chữ số còn lại.
Do đó trong trường hợp này có 4.6 = 24 số tạo thành.
Trường hợp chữ số 2 đứng bên trái chữ số 1 đứng kề bên phải
Hoàn toàn tương tự như trên ta cũng có 24 số được tạo thành.
Suy ra N(A) = 24 + 24 = 48
Vậy \(P(A)=\frac{N(A)}{N(\Omega )}=\frac{48}{120}=\frac{2}{5}\) -
-
Câu 9:
Tìm tất cả các giá trị nguyên của m để hệ phương trình sau có nghiệm:
\(\left\{\begin{matrix} x^2-4(2x-m^2-2m-2)=y(8-2x-y)\\ x^2-12x+y(y-2x+12)+40=4m(m+1) \end{matrix}\right.\)-
Hệ phương trình đã cho tương đương với hệ:
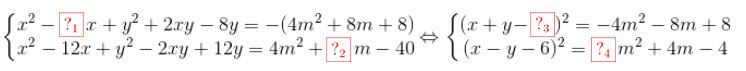
Suy ra hệ phương trình có nghiệm khi và chỉ khi
Vì m là số nguyên nên m = - 2Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Hệ phương trình đã cho tương đương với hệ:
\(\left\{\begin{matrix} x^2-8x+y^2+2xy-8y=-(4m^2+8m+8)\\ x^2-12x+y^2-2xy+12y=4m^2+4m-40 \end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} (x+y-4)^2=-4m^2-8m+8\\ (x-y-6)^2=4m^2+4m-4 \end{matrix}\right.\)
Suy ra hệ phương trình có nghiệm khi và chỉ khi
\(\left\{\begin{matrix} \\ -4m^2-8m+8\geq 0\\ 4m^2+4m-4\geq 0\\ \\ \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \\ m^2+2m-2\geq 0\\ m^2+m-1\geq 0\\ \\ \end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} -1-\sqrt{3}\leq m\leq -1+\sqrt{3}\\ \bigg \lbrack\begin{matrix} m\geq \frac{-1+\sqrt{5}}{2}\\ m\leq \frac{-1-\sqrt{5}}{2} \end{matrix}\\ \end{matrix}\right.\)
Vì m là số nguyên nên m = - 2 -




.JPG)

