Câu hỏi trắc nghiệm (9 câu):
-
Câu 1:
Cho hàm số \(y=\frac{2x+1}{x+1}\)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm các giá trị của m để đường thẳng y = mx + 2m + 1 cắt (C) tại hai điểm phân biệt A, B.Với giá trị nào của m thì khoảng cách từ hai điểm A và B đến trục hoành bằng nhau.-
1. Học sinh tự giải
2.
Đường thẳng y = mx + 2m +1 cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi pt có 2 nghiệm phân biệt

có hai nghiệm phân biệt khác (
 )
)
và
Gọi A (x1; y1), B(x2; y2) với x1, x2 là nghiệm của pt (1) và y1 = mx1 +2m +1, y2 = mx2 +2m + 1
Theo giả thiết ta suy ra

Theo định lý Vi – ét ta cónên từ (2) ta có:

 thỏa mãn (*)
thỏa mãn (*)
Vậy với m = thì đường thẳng y = mx +
thì đường thẳng y = mx +  m +
m +  cắt (C) tại hai điểm phân biệt.
cắt (C) tại hai điểm phân biệt.Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:1. Học sinh tự giải
2.
Đường thẳng y = mx + 2m +1 cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi pt có 2 nghiệm phân biệt
\(\frac{2x+1}{x+1}=mx+2m+1\Leftrightarrow mx^2+(3m-1)x+2m=0(1)\) có hai nghiệm phân biệt khác (-1)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0,\Delta =m^2-6m+1> 0\\ m-3m+1+2m\neq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>3+2\sqrt{2}\\ m<3-2\sqrt{2} \end{matrix}\right.\) và \(m\neq 0 (*)\)
Gọi A (x1; y1), B(x2; y2) với x1, x2 là nghiệm của pt (1) và y1 = mx1 +2m +1, y2 = mx2 +2m + 1
Theo giả thiết ta suy ra \(\left | y_1 \right |=\left | y_2 \right |\Leftrightarrow \bigg \lbrack\begin{matrix} y-1=y_2\\ y-1=-y_2 \end{matrix}\Rightarrow y_1+y_2=0\)
\(\Leftrightarrow m(x_1+x_2)+4m+2=0 \ \ (2)\)
Theo định lý Vi – ét ta có \(x_1+x_2=\frac{1-3m}{m}\) nên từ (2) ta có: \(1 - 3m + 4m + 2 = 0 \Leftrightarrow m = - 3\) thỏa mãn (*)
Vậy với m = -3 thì đường thẳng y = mx + 2m + 1 cắt (C) tại hai điểm phân biệt. -
-
Câu 2:
1) Giải phương trình \(\sqrt{x(x+7)}+\sqrt{(x+7)(x+17)}+\sqrt{(x+7)(2+24)}=12+17\sqrt{2}\)
2) Một ngân hàng đề thi gồm 100 câu hỏi, mỗi đề thi gồm 5 câu hỏi được chọn từ ngân hàng đề thi này. Một học sinh thuộc 80 câu trong 100 câu của ngân hàng đề thi. Tìm xác suất để học sinh đó rút ngẫu nhiên được một đề thi trong đó có đúng 4 câu mình đã thuộc
Lời giải:1. Điều kiện \(\bigg \lbrack \begin{matrix} x\geq 0\\ x\leq -\ 24 \end{matrix}\) Đặt \(t=x+12\Rightarrow \bigg \lbrack \begin{matrix} t\geq 12\\ t\leq -12 \end{matrix}\)
Phương trình trở thành \(\small f(x)=\sqrt{(t-12)(t-5)}+\sqrt{(t+5)(t-5)}+\sqrt{(+-12)(t+5)}= 12+17\sqrt{2}\)
Suy ra f(t) = f(-t), do đó f(t) là hàm số của số chẵn trên tập \(\small D = (-\infty ; -12] \cup [12; +\infty )\) nên chỉ cần xét trên \(\small [12; +\infty )\)
Ta có: \(\small f'(t)=\frac{2t-17}{2\sqrt{(t-12)(t-5)}}+\frac{t}{\sqrt{(t+5)(t-5)}}+\frac{2t+17}{2\sqrt{(t+12)(t+5)}}> 0\) với mọi giá trị \(\small t\in (12;+\infty )\)
Suy ra f(t) đồng biến trên \((12;+\infty )\) nên \(f(t)=12+17\sqrt{2}\) có nhiều nhất một nghiệm thuộc \(\small \left [12;+\infty )\)
Do f(t) là hàm số chẵn nên t = -13 là nghiệm duy nhất của phương trình trên \(\small \left [12;+\infty )\)
Vậy nghiệm của phương trình là x =1, x = -25.
2. Số phần tử của không gian mẫu là \(N(\Omega ) = C_{100}^{5}\)
Gọi A là biến cố mà học sinh rút được đề thi trong đó có đúng 4 câu đã thuộc.
Khi đó \(N(A) = C_{80}^{4}.C_{20}^{1}\)Vậy \(P(A) = \frac{N(A)}{N(\Omega )}=\frac{C_{80}^{4}.C_{20}^{1}}{C_{100}^{5}}\)
-
Câu 3:
Giải phương trình: \(sin3x + sin5x = 2(cos^2 2x- sin^23x)\)
Lời giải:Phương trình tương đương với \(sin3x+sin5x=2(\frac{cos4x+1}{2}-\frac{1-cos6x}{2})\)
\(\Leftrightarrow sin3x + sin5x = cos4x + cos6x \Leftrightarrow 2sin4x.cosx = 2cos5x.cosx\)
\(\Leftrightarrow cosx(cos5x - sin4x)=0\Leftrightarrow\bigg \lbrack \begin{matrix} cosx=0\\ cos5x=sin4x \end{matrix}\)
Với \(cosx = 0 \Leftrightarrow x=\frac{\pi}{2}+k\pi (k\in Z)\)
Với \(cos5x = sin4x\) \(\Leftrightarrow cos5x = cos(\frac{\pi }{2}-4x)\)
\(\Leftrightarrow \bigg \lbrack \begin{matrix} 5x=\frac{\pi }{2}-4x+2k\pi \\ 5x=-\frac{\pi }{2}+4x+2k\pi \end{matrix}\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x=\frac{\pi }{18}+\frac{2k\pi }{9}\\ x=-\frac{\pi }{2}+2k\pi \end{matrix}, (k\in Z)\)
Vậy nghiệm của phương trình là \(x\in \left \{ \frac{\pi }{2}+k\pi, \ x=\frac{\pi }{18}+\frac{2k\pi }{9}/k\in Z \right \}\)
-
Câu 4:
Tính tích phân \(I=\int_{1}^{\sqrt{3}}\frac{ln(x^2+1)}{x^2}dx\)
Lời giải:Ta có: \(\small I = -\int_{1}^{\sqrt{3}}ln(x^2+1)d\frac{1}{x}=-\frac{1}{x}ln(x^2+1)\bigg | \begin{matrix} \sqrt{3}\\ 1 \end{matrix}+\int_{1}^{\sqrt{3}}\frac{1}{x}d\ ln(x^2+1)\)
\(\small =\frac{3-2\sqrt{3}}{3}ln2+2\int_{1}^{\sqrt{3}}\frac{dx}{x^2+1}\)
Tính \(\small \int_{1}^{\sqrt{3}}\frac{dx}{x^2+1}.\) Đặt \(\small x = tant,\) khi đó \(\small dx=\frac{dt}{cos^2t};\) với x = 1 thì \(\small t= \frac{\pi }{4}\) với \(\small x=\sqrt{3}\) thì \(\small t=\frac{\pi }{3}\)
Suy ra \(\small \int_{1}^{\sqrt{3}}\frac{dx}{x^2+1} = \int_{\frac{\pi }{4}}^{\frac{\pi }{3}}dt=\frac{\pi }{3}-\frac{\pi }{4}=\frac{\pi }{12}\)
\(\small \Rightarrow 2\int_{1}^{\sqrt{3}}\frac{dx}{x^2+1}=\frac{\pi }{6}.\)
Vậy \(\small I = \frac{3-2\sqrt{3}}{3}ln2+\frac{\pi }{6}\)
-
Câu 5:
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a và góc giữa đường thẳng AA’ và mặt phẳng (ABC) là 600. Tính thể tích khối tứ diện ACA’B’.
Lời giải: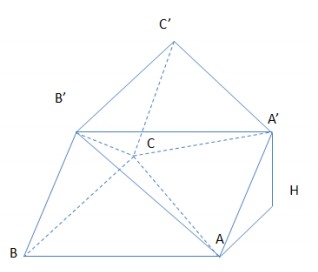
Kí hiệu h và V tương ứng là chiều cao và thể tích của khối lăng trị đã cho.
Ta có \(\small V_{ACA'B'}=\frac{1}{2}.V_{B'ACC'A'}=\frac{1}{2}=\frac{1}{2}(V-\frac{1}{3}.h.S_{ABC})=\frac{1}{2}(V-\frac{1}{3}V)=\frac{1}{3}V\)
Gọi H là hình chiếu vuông góc của A’ trên (ABC).
Ta có A'H = h và \(\small \widehat{A'AH}=60^{0}\). Suy ra \(\small h = A'A.sin60^{0}=a\sqrt{3}\)
Do đó, \(\small V=h.S_{ABC}=a\sqrt{3}.\frac{a^2\sqrt{3} }{4}= \frac{3a^3}{4}\)
Vậy \(\small V_{ACA'B'}=\frac{a^3}{4}\)
-
Câu 6:
Trong mặt phẳng với hệ tọa độ Oxyz, cho tam giác ABC có H là trực tâm, \(C(3;\frac{3}{2})\) . Đường thẳng AH có phương trình 2x – y + 1 = 0. Đường thẳng d đi qua H, cắt các đường thẳng AB, AC lần lượt tại P và Q (khác điểm A) thỏa mãn HP = HQ và có phương trình: 2x – 3y + 7 = 0. Tìm tọa độ các đỉnh A và B.
-
Qua C kẻ đường thẳng song song với d cắt AB tại N và cắt AH tại K, do HP = HQ nên KC = KN
Gọi M là trung điểm của BC. Ta có KM // NB, suy ra KM vuông góc với CH nên M là trực tâm ∆CHK
Tóm lại xác định được K, M nên suy ra xác định được A, B.
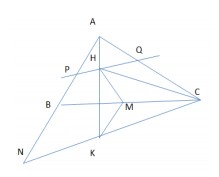
Đường thẳng CK:
Tọa độ điểm K là nghiệm của hệ pt:
. Do K là trung điểm của CN nên

Tọa độ điểm H là nghiệm của hệ pt
Đường thẳng qua H vuông góc với d: 3x + 2y – = 0
= 0
Đường thẳng qua C vuông góc với AH: x + 2y – = 0
= 0Tọa độ điểm M là nghiệm của hệ pt:
Suy ra
Đường thẳng BN: 4x – y + = 0.
y + = 0.
Tọa độ điểm A là nghiệm của hệ Pt
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Qua C kẻ đường thẳng song song với d cắt AB tại N và cắt AH tại K, do HP = HQ nên KC = KN
Gọi M là trung điểm của BC. Ta có KM // NB, suy ra KM vuông góc với CH nên M là trực tâm ∆CHK
Tóm lại xác định được K, M nên suy ra xác định được A, B.

Đường thẳng CK: \(2x - 3y - \frac{3}{2} = 0\)
Tọa độ điểm K là nghiệm của hệ pt: \(\left\{\begin{matrix} 2x-3y-\frac{3}{2}\\ 2x-y+1=0 \end{matrix}\right.\)
\(\Rightarrow K\left ( -\frac{9}{8};-\frac{5}{4} \right )\). Do K là trung điểm của CN nên \(N(-\frac{21}{4};-4)\)
Tọa độ điểm H là nghiệm của hệ pt \(\left\{\begin{matrix} 2x-2y+7=0\\ 2x-y+1=0 \end{matrix}\right.\Rightarrow H(1;3)\)
Đường thẳng qua H vuông góc với d: 3x + 2y – 9 = 0
Đường thẳng qua C vuông góc với AH: x + 2y – 6 = 0Tọa độ điểm M là nghiệm của hệ pt: \(\left\{\begin{matrix} 3x-y-9=0\\ x+2y-6=0 \end{matrix}\right.\Rightarrow M(\frac{3}{2};\frac{9}{4})\)
Suy ra \(B(0;3)\)
Đường thẳng BN: 4x – 3y + 9 = 0.
Tọa độ điểm A là nghiệm của hệ Pt \(\left\{\begin{matrix} 2x-y+1=0\\ 4x-3y+9=0 \end{matrix}\right.\Rightarrow A(3;7)\) -
-
Câu 7:
Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): x – 2y + z + 5 = 0.
1) Gọi giao điểm của mặt phẳng (P) với các trục Ox và Oz lần lượt tại X và Z. Tính diện tích của tam giác OXZ.
2) Lập phương trình mặt phẳng (α) vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng (P1): x – 2z = 0 và (P2): 3x – 2y + z – 3 = 0.-
1.
Điểm X thuộc OxX(x; 0; 0) và điểm X thuộc (P) nên ta có: x –
 . 0 + 0 + 5 = 0
. 0 + 0 + 5 = 0

Điểm Z thuộc Oz Z(0;0;z) và điểm Z thuộc (P) nên ta có: 0 - 2.0 + z + 5 = 0Z(0;0;
 )
) OZ =

Vậy
2.
Gọivà

lần lượt là véc tơ pháp tuyến của (P1) , (P2).
Khi đó vec tơ chỉ phương của d là
Véc tơ pháp tuyến của (P) là, suy ra vecto pháp tuyến của
là

Ta nhận thấythuộc đường thẳng d. Suy ra phương trình mặt phẳng (α) là: 11x – 2y – 15z –
 = 0.
= 0.Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:1.
Điểm X thuộc Ox \(\Leftrightarrow\) X(x; 0; 0) và điểm X thuộc (P) nên ta có: x – 2. 0 + 0 + 5 = 0
\(\Rightarrow X(-5;0;0)\Rightarrow OX=5\)
Điểm Z thuộc Oz Z(0;0;z) và điểm Z thuộc (P) nên ta có: 0 - 2.0 + z + 5 = 0 \(\Rightarrow\) Z(0;0;-5) \(\Rightarrow\) OZ = 5.
Vậy \(S_{OXZ}=\frac{1}{2}.OX.OZ=\frac{25}{2}\)
2.
Gọi \(\overrightarrow{n_1}(1;0;-2)\) và \(\overrightarrow{n_2}(3;-2;1)\) lần lượt là véc tơ pháp tuyến của (P1) , (P2).
Khi đó vec tơ chỉ phương của d là \(\overline{u}=\left [\overline{n_2},\overline{n_1} \right ]=(4;7;2)\)
Véc tơ pháp tuyến của (P) là \(\overline{n_P}=(1;-2;1)\), suy ra vecto pháp tuyến của \((\alpha )\) là \(\overline{n_\alpha }=\left [\overline{u_d},\overline{n_P} \right ]=(11;-2;-15)\)
Ta nhận thấy \(M(0;-\frac{3}{2};0)\) thuộc đường thẳng d. Suy ra phương trình mặt phẳng (α) là: 11x – 2y – 15z – 3 = 0 . -
-
Câu 8:
Tìm mô đun của số phức z, biết \((2+i)(1-iz)+\frac{2(1+2i)}{1+i}=(3-2i)z\)
Lời giải:Ta có \(\small (2+i)(1-iz)+\frac{2(1+2i)}{1+i}=(3-2i)z\Leftrightarrow 2+i+1(1-2i)z+3+i=(3-2i)z\)
\(\small \Leftrightarrow 5+2i=2z\)
Suy ra \(\small z=\frac{5}{2}+i.\) Khi đó \(\small \left | z \right |=\frac{\sqrt{29}}{2}\)
-
Câu 9:
Giải bất phương trình\(\small e^{1+\sqrt{x}}+\sqrt{1+\sqrt{x}}+\frac{1}{\sqrt{1+\sqrt{x}}}> e^{2x-4\sqrt{x}+3}+\sqrt{2x-4\sqrt{x+3}}+\frac{1}{\sqrt{2x-4\sqrt{x}+3}}\)
Lời giải:Điều kiện \(\small x \geq 0\)
Xét hàm số \(\small f(t)=e^t+\sqrt{t}+\frac{1}{\sqrt{t}}\) với \(\small t\in \left [ 1;+\infty )\)Ta có \(\small f'(t)=e^t+\sqrt{t}+\frac{t-1}{2t\sqrt{t}}> 0\) với \(\small t\in \left [ 1;+\infty )\)
Do đó từ bất phương trình đã cho tương đương với \(\small 1+\sqrt{x}> 2x-4\sqrt{x}+3\)
\(\small \Leftrightarrow 2x-5\sqrt{x}+2< 0\Leftrightarrow \frac{1}{2}< \sqrt{x}< 2\Leftrightarrow \frac{1}{4}< x< 4\)
Vậy tập nghiệm của bất phương trình gồm các giá trị của x thỏa mãn





