Đề thi THPT Quốc gia năm 2015 môn Toán

YOMEDIA

Câu hỏi trắc nghiệm (10 câu):

Câu 1:

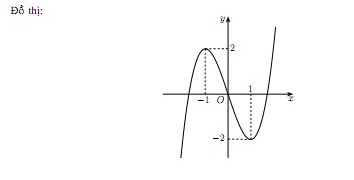
Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = x^3-3x$
- Tập xác định: D = R
  
  Sự biến thiên:
  - Chiều biến thiên: $y' = 3x^2-3; y'=0\Leftrightarrow x=\pm$
  Các khoảng đồng biến: $(-\infty ;$ $)$ và $(1;$ $)$ ; khoảng nghịch biến: (-1; 1)
  - Cực trị: Hàm số đạt cực đại tại x = -1, y_CĐ= ; đạt cực tiểu tại x = 1, y_CT=
  - Giới hạn tại vô cực: $\lim_{x\rightarrow -\infty }y=- \infty ; \lim_{x\rightarrow +\infty }y=$
  
  Bảng biến thiên
  
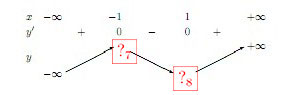
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  Ghi chú. Dấu $+\infty$ được ghi là +vc; dấu $-\infty$ được ghi là −vc.
  = = = = = = = =
Lời giải:
Tập xác định: D = R

Sự biến thiên:
- Chiều biến thiên: $y' = 3x^2-3; y'=0\Leftrightarrow x=\pm 1$
Các khoảng đồng biến: $(-\infty ;-1)$ và $(1;+\infty )$; khoảng nghịch biến: (-1; 1)
- Cực trị: Hàm số đạt cực đại tại x = -1, y_CĐ= 2; đạt cực tiểu tại x = 1, y_CT= -2
- Giới hạn tại vô cực: $\lim_{x\rightarrow -\infty }y=- \infty ; \lim_{x\rightarrow +\infty }y=+ \infty$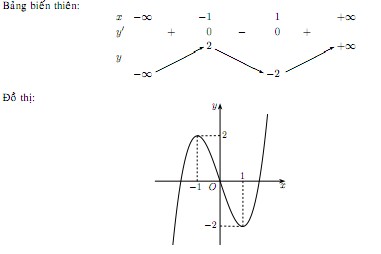
Câu 2:

Tìm giá trị lớn nhất và nhỏ nhất của hàm số $f(x)=x+\frac{4}{x}$ trên đoạn $\left [ 1;3 \right ]$
- Ta có f(x) xác định và liên tục trên đoạn $\left [ 1;3 \right ]$ $f'(x)=$ $-\frac{4}{x^2}$
  Với $x\epsilon \left [ 1;3 \right ], f(x)=$ $\Leftrightarrow x=$
  
  Ta có $f(1) =$ $, f(2)=$ $, f(3)=$
  
  Giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn $\left [ 1;3 \right ]$ lần lượt là và
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
Ta có f(x) xác định và liên tục trên đoạn $\left [ 1;3 \right ]$ $f'(x)=1-\frac{4}{x^2}$
Với $x\epsilon \left [ 1;3 \right ], f(x)=0\Leftrightarrow x=2$

Ta có $f(1) =5, f(2)=4, f(3)=\frac{13}{3}$

Giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn $\left [ 1;3 \right ]$ lần lượt là 5 và 4
Câu 3:

a) Cho số phức z thỏa mãn (1 - i)z - 1 +5i = 0. Tìm phần thực và phần ảo của z.
b) Giải phương trình $log_{2}(x^2+x+2)=3$
- a) Ta có $(1 - i)z - 1 +5i = 0\Leftrightarrow$ z= - i
  Do đó số phức z có phần thực bằng , phần ảo bằng
  b) TXĐ: $\mathbb{R}$
  
  Phương trình đã cho tương đương với $x^2+x+2=$ $\Leftrightarrow x^{2}+x-$ $=0$
  $\Leftrightarrow \bigg \lbrack \begin{matrix} x=2\\ x=-3 \end{matrix}$
  
  Vậy nghiệm của phương trình là x = ; x =
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
a) Ta có $(1 - i)z - 1 +5i = 0\Leftrightarrow z=3-2i$
Do đó số phức z có phần thực bằng 3, phần ảo bằng - 2
b) TXĐ: $\mathbb{R}$

Phương trình đã cho tương đương với $x^2+x+2=8$$\Leftrightarrow x^{2}+x-6=0$
$\Leftrightarrow \bigg \lbrack \begin{matrix} x=2\\ x=-3 \end{matrix}$

Vậy nghiệm của phương trình là x = 2; x = -3
Câu 4:

Tính tích phân $I=\int_{0}^{1} (x-3)e^xdx.$
- Đặt $u = x -$ $; dv = e^xdx$ . Suy ra $du = dx; v=$ [q2[ $e^x$
  Khi đó $I=$ $(x-3)e^x\bigg | \begin{matrix} 1\\ 0 \end{matrix}-$ $\int_{0}^{1}e^xdx$
  
  $=$ $(x-3)e^x\bigg | \begin{matrix} 1\\ 0 \end{matrix}$ $-$ $e^x\bigg | \begin{matrix} 1\\ 0 \end{matrix}$
  
  $=$ $-$ $e$
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
Đặt $u = x - 3; dv = e^xdx$. Suy ra $du = dx; v=e^x$
Khi đó $I= (x-3)e^x\bigg | \begin{matrix} 1\\ 0 \end{matrix}-\int_{0}^{1}e^xdx$

$=$ $(x-3)e^x\bigg | \begin{matrix} 1\\ 0 \end{matrix}$$- e^x\bigg | \begin{matrix} 1\\ 0 \end{matrix}$

$=-4-3e$
Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;-2;1), B(2;1;3) và mặt phẳng $(P): x-y+2z-3=0.$ Viết phương trình đường thẳng AB và tìm tọa độ giao điểm của đường thẳng AB với mặt phẳng (P).
- Ta có $\overrightarrow{AB} = (1;$ $;2)$
  
  Đường thẳng AB có phương trình $\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{3}$
  
  Gọi M là giao điểm của AB và (P). Do M thuộc AB nên $M($ $+t;$ $+3t;1+$ $t)$
  M thuộc (P) nên $+t-($ $+3t)+$ $(1+2t)-3=0$ , suy ra $t=$ . Do đó M (0;-5;-1)
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
Ta có $\overrightarrow{AB} = (1;3;2)$

Đường thẳng AB có phương trình $\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{3}$

Gọi M là giao điểm của AB và (P). Do M thuộc AB nên $M(1+t;-2+3t;1+3t)$
M thuộc (P) nên $1+t-(-2+3t)+2(1+2t)-3=0$, suy ra $t=-1$. Do đó M (0;-5;-1)
Câu 6:

a) Tìm giá trình của biểu thức $P=(1-3cos2\alpha )(2+3cos2\alpha )$ biết $sin\alpha =\frac{2}{3}$
b) Trong đợt ứng phó dịch MERS-CoV, Sở Y tế thành phố đã chọn ngẫu nhiên 3 đội phòng chống dịch cơ động trong số 5 của Trung tâm y tế dự phòng thành phố và 20 đội của các Trung tâm y tế cơ sở để kiểm tra công tác chuẩn bị. Tính xác xuất để có ít nhất 2 đội của các Trung tâm y tế cơ sở được chọn
- a) Ta có $cos2\alpha =$ $-2sin^2\alpha =$
  
  Suy ra $P = (1-\frac{1}{3})($ $+\frac{1}{3})=$
  
  b) Số phần tử của không gian mẫu là $C_{25}^{3}=$
  
  Số kết quả thuận lợi cho biến cố "có ít nhất 2 đội của các Trung tâm y tế cơ sở" là $C_{20}^{2}.C_{5}^{1}+C_{20}^{3}=$
  
  Xác suất cần tính là $p=\frac{2090}{2300}=$
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
a) Ta có $cos2\alpha =1-2sin^2\alpha =\frac{1}{9}$

Suy ra $P = (1-\frac{1}{3})(2+\frac{1}{3})=\frac{14}{9}$

b) Số phần tử của không gian mẫu là $C_{25}^{3}=2300$

Số kết quả thuận lợi cho biến cố "có ít nhất 2 đội của các Trung tâm y tế cơ sở" là $C_{20}^{2}.C_{5}^{1}+C_{20}^{3}=2090$

Xác suất cần tính là $p=\frac{2090}{2300}=\frac{209}{230}$
Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45⁰ . Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB, AC.
- Ta có $\widehat{SCA}=(SC,(\widehat{ABCD}))=$
  
  Suy ra $SA=AC=$ $\sqrt{2}a$
  
  $V_{S.ABCD}=$ $SA.S_{ABCD}=$ $.\sqrt{2}.a^2=$ $\sqrt{2}a^3}$
  
  Kẻ đường thẳng d qua B và song song AC. Gọi M là hình chiếu vuông góc của A trên d; H là hình chiếu vuông góc của A trên SM. Ta có $SA \perp BM, MA \perp BM$ nên $AH \perp BM.$
  
  Suy ra $AH \perp (SBM).$
  
  Do đó d(AC,SB)=d(A,(SBM))=AH
  
  Tam giác SAM vuông tại A, có đường cao AH, nên $\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AM^2}=$ $\frac{1}{a^2}$
  
  Vậy d(AC, SB) = AH = $\frac{\sqrt{10}a}{5}$
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:

Ta có $\widehat{SCA}=(SC,(\widehat{ABCD}))=45^0$

Suy ra $SA=AC=\sqrt{2}a$

$V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{1}{3}.\sqrt{2}.a^2=\frac{\sqrt{2}a^3}{3}$

Kẻ đường thẳng d qua B và song song AC. Gọi M là hình chiếu vuông góc của A trên d; H là hình chiếu vuông góc của A trên SM. Ta có $SA \perp BM, MA \perp BM$ nên $AH \perp BM.$

Suy ra $AH \perp (SBM).$

Do đó d(AC,SB)=d(A,(SBM))=AH

Tam giác SAM vuông tại A, có đường cao AH, nên $\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AM^2}=\frac{5}{2a^2}$

Vậy d(AC, SB) = AH = $\frac{\sqrt{10}a}{5}$
Câu 8:

Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A. Gọi H là hình chiếu vuông góc của A trên cạnh BC; D là điểm đối xứng của B qua H; K là hình chiếu vuông góc của C trên đường thẳng AD. Giả sử H(-5;-5), K(9;-3) và trung điểm của cạnh AC thuộc đường thẳng x – y + 10 = 0. Tìm tọa độ điểm A.
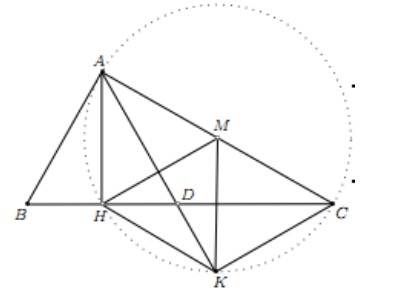
- Gọi M là trung điểm của AC. Ta có $MH=MK=$ $AC$ nên M thuộc đường trung trực của HK.
  Đường trung trực của HK có phương trình x + y - 10 = 0, nên tọa độ của M thỏa mãn hệ pt $\left\{\begin{matrix} x-y+10=0\\ 7x+y-10=0 \end{matrix}\right.$
  Suy ra M(0;)
  Ta có $\widehat{HKA}=\widehat{HCA}=\widehat{HBA}=\widehat{HAD}$ , nên $\Delta AHK$ cân tại H, suy ra HA = HK. Mà MA = MK, nên A đối xứng với K qua MH.
  Ta có: $\overrightarrow{MH} = (5;$ $)$ ; đường thẳng MH có phương trình 3x - y + = 0. Trung điểm AK thuộc MH và $AK\perp MH$ nên tọa độ điểm A thỏa mãn hệ $\left\{\begin{matrix} 3(\frac{x+9}{2})-(\frac{y-2}{2})+10=0\\ (x-9)+3(y+3)=0 \end{matrix}\right.$
  Suy ra A(;)
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:

Gọi M là trung điểm của AC. Ta có $MH=MK=\frac{AC}{2}$ nên M thuộc đường trung trực của HK.
Đường trung trực của HK có phương trình 7x + y - 10 = 0, nên tọa độ của M thỏa mãn hệ pt $\left\{\begin{matrix} x-y+10=0\\ 7x+y-10=0 \end{matrix}\right.$
Suy ra M(0;10)
Ta có $\widehat{HKA}=\widehat{HCA}=\widehat{HBA}=\widehat{HAD}$, nên $\Delta AHK$ cân tại H, suy ra HA = HK. Mà MA = MK, nên A đối xứng với K qua MH.
Ta có: $\overrightarrow{MH} = (5;15)$; đường thẳng MH có phương trình 3x - y + 10 = 0. Trung điểm AK thuộc MH và $AK\perp MH$ nên tọa độ điểm A thỏa mãn hệ $\left\{\begin{matrix} 3(\frac{x+9}{2})-(\frac{y-2}{2})+10=0\\ (x-9)+3(y+3)=0 \end{matrix}\right.$
Suy ra A(-15;5)
Câu 9:

Giải phương trình $\frac{x^2+2x-8}{x^2-2x+3}=(x+1)(\sqrt{x+2}-2)$ trên tập só thực.
- Điều kiện $x\geq$ . Phương trình cho tương ứng với
  $\frac{(x-2)(x-4)}{x^2-2x+3}=\frac{(x+1)(x-2)}{\sqrt{x+2}+2}\Leftrightarrow \bigg \lbrack \begin{matrix} x=2\\ \frac{x+4}{x^2-2x+3}=\frac{x+1}{\sqrt{x+2}-2} \end{matrix}$ (1)
  
  Ta có (1) $\Leftrightarrow (x+4)(\sqrt{x+2}+2)=(x+1)(x^2-$ $x+3)$
  $\Leftrightarrow (\sqrt{x+2}+2)\left [ (\sqrt{x+2})^2+2\right ]=\left [ (x-1) +2\right ]\left [ (x-1)^2+$ $\big ]$ (2)
  
  Xét hàm số $f(x)=(t+2)(t^2+$ $).$
  
  Ta có $f'(t)=3t^2+4t+$ suy ra $f'(t)> 0, \forall t\epsilon R$ , nên f(t) đồng biến trên R.
  Do đó (2) $\Leftrightarrow f(\sqrt{x+2})=f(x+$ $)\Leftrightarrow \sqrt{x+2}=x-$ $\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x^2-3x-1=0 \end{matrix}\right.$
  
  $\Leftrightarrow x=\frac{3+\sqrt{13}}{2}$
  Đối chiếu điều kiện, ta được nghiệm của phương trình đã cho là x = ; $x=\frac{3+\sqrt{13}}{2}$
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
Điều kiện $x\geq -2$. Phương trình cho tương ứng với
$\frac{(x-2)(x-4)}{x^2-2x+3}=\frac{(x+1)(x-2)}{\sqrt{x+2}+2}\Leftrightarrow \bigg \lbrack \begin{matrix} x=2\\ \frac{x+4}{x^2-2x+3}=\frac{x+1}{\sqrt{x+2}-2} \end{matrix}$ (1)

Ta có (1) $\Leftrightarrow (x+4)(\sqrt{x+2}+2)=(x+1)(x^2-2x+3)$
$\Leftrightarrow (\sqrt{x+2}+2)\left [ (\sqrt{x+2})^2+2\right ]=\left [ (x-1) +2\right ]\left [ (x-1)^2+2 \right ]$ (2)

Xét hàm số $f(x)=(t+2)(t^2+2).$

Ta có $f'(t)=3t^2+4t+2$ suy ra $f'(t)> 0, \forall t\epsilon R$, nên f(t) đồng biến trên R.
Do đó (2) $\Leftrightarrow f(\sqrt{x+2})=f(x+1)\Leftrightarrow \sqrt{x+2}=x-1\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x^2-3x-1=0 \end{matrix}\right.$

$\Leftrightarrow x=\frac{3+\sqrt{13}}{2}$
Đối chiếu điều kiện, ta được nghiệm của phương trình đã cho là x = 2; $x=\frac{3+\sqrt{13}}{2}$
Câu 10:

Cho các số thực a, b, c thuộc đoạn [1;3] và thỏa mãn điều kiện a + b + c = 6.
Tìm giá trị lớn nhất của biểu thức. $P=\frac{a^2b^2+b^2c^2+c^2a^2+12abc+72}{ab+bc+ca}$
- Đặt $t=ab+bc+ca$
  
  Ta có $36=(a+b+c)^2=$ $\left [ (a-b)^2+(b-c)^2+(c-a)^2 \right ]+3t\geq 3t$ . Suy ra $t\leq 12$ .
  
  Mặt khác, $(a-1)(b-1)(c-1)\geq 0$ nên $abc\geq ab+bc+ca-5=t-5$ và $(3-a)(3-b)(3-c)\geq 0$ ,
  
  nên $t=3(ab+bc+ca)\geq abc+27\geq t+22$ . Suy ra $t\geq$ .
  
  Vậy $t\epsilon \left [ 11;12 \right ]$
  
  Khi đó
  
  $P=\frac{a^2b^2+b^2c^2+c^2a^2+2abc(a+b+c)+72}{ab+bc+ca}-\frac{abc}{2}$
  
  $=\frac{(ab+bc+ca)^2+72}{ab+bc+ca}-\frac{abc}{2}\leq \frac{t^2+72}{t}-\frac{t-5}{2}=\frac{t^2+5t+144}{2t}$
  
  Xét hàm số $f(t)=\frac{t^2+5t+144}{2t}$ , với $t\epsilon \left [ 11;12 \right ]$ . Ta có $f'(t)=\frac{t^2-144}{2t^2}$
  
  Do đó $f'(t)\leq 0,\forall t \epsilon \left [ 11;12 \right ]$ , nên $f'(t)$ nghịch biến trên đoạn $\left [ 11;12 \right ]$
  
  Suy ra $f(t)\leq f(11)=\frac{160}{11}$ . Do đó $P\leq$
  
  Ta có a = , b = 2, c = thỏa nãm điều kiện của bài toán và khi đó $P=$ .
  
  Vậy giá trị lớn nhất của P bằng .
  
  Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
  = = = = = = = =
Lời giải:
Đặt $t=ab+bc+ca$

Ta có $36=(a+b+c)^2=\frac{1}{2}\left [ (a-b)^2+(b-c)^2+(c-a)^2 \right ]+3t\geq 3t$. Suy ra $t\leq 12$.

Mặt khác, $(a-1)(b-1)(c-1)\geq 0$ nên $abc\geq ab+bc+ca-5=t-5$ và $(3-a)(3-b)(3-c)\geq 0$, nên $3t=3(ab+bc+ca)\geq abc+27\geq t+22$. Suy ra $t\geq 11$.

Vậy $t\epsilon \left [ 11;12 \right ]$

Khi đó

$P=\frac{a^2b^2+b^2c^2+c^2a^2+2abc(a+b+c)+72}{ab+bc+ca}-\frac{abc}{2}$

$=\frac{(ab+bc+ca)^2+72}{ab+bc+ca}-\frac{abc}{2}\leq \frac{t^2+72}{t}-\frac{t-5}{2}=\frac{t^2+5t+144}{2t}$

Xét hàm số $f(t)=\frac{t^2+5t+144}{2t}$, với $t\epsilon \left [ 11;12 \right ]$. Ta có $f'(t)=\frac{t^2-144}{2t^2}$

Do đó $f'(t)\leq 0,\forall t \epsilon \left [ 11;12 \right ]$, nên $f'(t)$ nghịch biến trên đoạn $\left [ 11;12 \right ]$

Suy ra $f(t)\leq f(11)=\frac{160}{11}$. Do đó $P\leq \frac{160}{11}$

Ta có a = 1, b = 2, c = 3 thỏa nãm điều kiện của bài toán và khi đó $P=\frac{160}{11}$.

Vậy giá trị lớn nhất của P bằng $\frac{160}{11}$.