Dạng 5: Vận tốc trung bình - Tốc độ trung bình

Thông qua bài học này, học sinh biết được công thức tính vận tốc trung bình, tốc độ trung bình. Từ đó tìm vận tốc trung bình - tốc độ trung bình của vật dao động điều hòa trong một quá trình nào đó.

Hôm nay chúng ta qua tiếp dạng Vận tốc trung bình - Tốc độ trung bình của ứng dụng giải bài toán dao động điều hòa. Hai khái niệm này học sinh rất dễ nhầm.

Ở bài toán vật chuyển động trong dao động điều hòa, các em thường nhầm giữa vận tốc và tốc độ. Khi nói đến vận tốc là nói đến đại lượng vectơ, vận tốc tại vị trí, tại thời điểm là vectơ tại vị trí, tại thời điểm đó. Còn tốc độ là độ lớn của vận tốc tại vị trí, thời điểm đó. Thực ra khái niệm Vận tốc trung bình - Tốc độ trung bình các em đã được học từ lớp 10.

* 
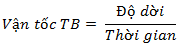
\(\Delta x = x_2 - x_1\): Độ dời
\(\Delta t = t_2 - t_1\): Thời gian
\(\Rightarrow v_{TB} = \frac{\Delta x}{\Delta t} = \frac{x_2 - x_1}{t_2 - t_1}\)
VD:


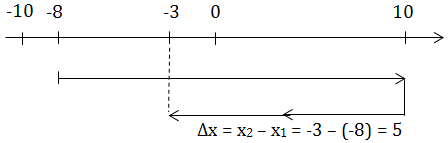
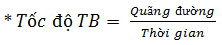
S: Quãng đường
\(\Delta t = t_2 - t_1\): Thời gian
\(\Rightarrow \overline{v} = \frac{S}{\Delta t}\)
VD:

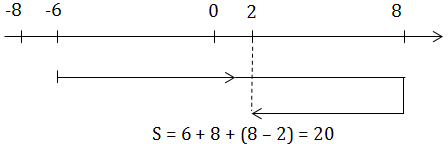
VD1: Một vật DĐĐH với phương trình \(x = 5.cos\pi t\) (cm). Tìm vận tốc trung bình và tốc độ trung bình trong 2016 chu kỳ?
Giải:
Trong 1T: \(\left\{\begin{matrix} \Delta x = 0 \Rightarrow v_{TB} = \frac{\Delta x}{\Delta t} = 0\\ S = 4A \Rightarrow \overline{v} = \frac{S}{\Delta t} = \frac{4A}{T} \ \ \\ \Delta t = T \hspace{3,1cm} \end{matrix}\right.\)
\(\overline{v} = \frac{4A}{T} = 4Af = 4.\frac{\omega }{2 \pi }.A = \frac{2}{\pi}.\omega A =\frac{2}{\pi}.v_{max}\)
Trong 2016T: \(\left\{\begin{matrix} \Delta x = 0 \ \ \ \ \ \ \\ S = 2016.4A \\ \Delta t = 2016.T \end{matrix}\right. \Rightarrow \left\{\begin{matrix} v_{TB} = 0\\ \overline{v} = \frac{4A}{T} \end{matrix}\right.\)

VD2: Một vật DĐĐH khi qua vị trí cân bằng đạt tốc độ \(20\pi \frac{cm}{s}\). Tìm tốc độ trung bình trong 2015 chu kỳ?
Giải:
\(|v_{max}| = \omega A = 20 \pi \frac{cm}{s}\)
Trong \(2015T \Rightarrow \overline{v} = \frac{4A}{T} = ... = \frac{2}{\pi}.v_{max} = 40 \frac{cm}{s}\)
* Chú ý: Trong thời gian \(\Delta t = (2K + 1)\frac{T}{2}\)
\(\Rightarrow S = (2K + 1).2A \Rightarrow \overline{v} = \frac{S}{\Delta t} = \frac{(2K+ 1).2A}{(2K+ 1).\frac{T}{2}} = \frac{4A}{T}\)