GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
1. Thể tích khối hộp ABCD.A'B'C'D' là
\(V_{ABCD.A'B'C'D'}=\left | \left [ \overrightarrow{AB}; \overrightarrow{AC} \right ]. \overrightarrow{AA'}\right |= \left | \left [ \overrightarrow{AB}; \overrightarrow{AD} \right ].\overrightarrow{AA'} \right |\)
2. Thể tích khối tứ diện ABCD.
\(V_{ABCD}=\frac{1}{6}\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] . \overrightarrow{AD} \right |\)

II. Bài tập
VD1: Tính thể tích của khối tứ diện ABCD A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;0)
Giải
\(\overrightarrow{AB}=(-1;1;0)\)
\(\overrightarrow{AB}=(-1;0;1)\)
\(\left [ \overrightarrow{AB}; \overrightarrow{AC} \right ]= \left ( \begin{vmatrix} 1 \ \ 0\\ 0 \ \ 1 \end{vmatrix}; \begin{vmatrix} 0 \ \ -1\\ 1 \ \ -1 \end{vmatrix}; \begin{vmatrix} -1 \ \ 1\\ -1 \ \ 0 \end{vmatrix} \right )=(1;1;1)\)
\(\overrightarrow{AD}=(-3;1;0)\)
\(V_{ABCD}=\frac{1}{6}\left | \left [ \overrightarrow{AB};\overrightarrow{AC} .\overrightarrow{AD}\right ] \right |=\frac{1}{6}\left | -2.1+1.1+0.1 \right |= \frac{2}{6}=\frac{1}{3}\)
b) Tính độ dài đường cao kẻ từ D của khối tứ diện ABCD.
Kẻ đường cao DH
\(DH=\frac{3V_{D.ABC}}{S_{\Delta ABC}}=\frac{3V_{ABCD}}{S_{ ABC}}\)
\(=\frac{1}{\frac{1}{2}\left | \left [ \overrightarrow{AB}; \overrightarrow{AC} \right ] \right |}=\frac{2}{\sqrt{1^2+1^2+1^2}}=\frac{2}{\sqrt{3}}\)
VD2: Trong không gian với hệ tọa độ Đềcac Oxyz, cho hình chóp S.ABCD, có đáy ABCD là hình thoi, AC cắt BD tại gốc tọa độ O. A(2;0;0), B(0;1;0), S(0;0; \(2\sqrt{2}\)). M là trung điểm SC. Mp(ABM) cắt SD tại N. Tính VSABMN
Giải
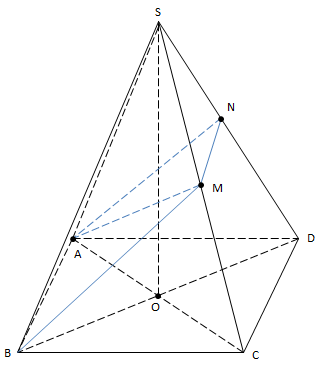
\(O=AC\cap BD\) nên O là trung điểm AC
\(\left\{\begin{matrix} x_C=2x_0-x_A=-2\\ y_C=2y_0-y_A=0\\ z_C=2z_0-z_A=0 \end{matrix}\right.\)
C(-2;0;0)
M là trung điểm SC nên \(M(-1;0;\sqrt{2})\)
O là trung điểm BD nên
\(\left\{\begin{matrix} x_D=2x_0-x_B=0\\ y_D=2y_0-y_B=-1\\ z_D=2z_0-z_B=0 \end{matrix}\right.\Rightarrow D(0;-1;0)\)
AB // CD nên gt (ABM) với (SCD) là đường thẳng qua M và song song CD.
Mặt khác M là trung điểm SC nên N là trung điểm SD. Do đó \(N\left ( 0;-\frac{1}{2};\sqrt{2} \right )\)
\(V_{S.ABMN}=V_{S.AMB}+V_{S.AMN}\)
\(\overrightarrow{SA}=(2;0;-2\sqrt{2})\)
\(\overrightarrow{SM}=(-1;0;-\sqrt{2})\)
\(\left [ \overrightarrow{SA};\overrightarrow{SM} \right ] =\left ( \begin{vmatrix} 0 \ \ -2\sqrt{2}\\ 0 \ \ -\sqrt{2} \end{vmatrix}; \begin{vmatrix} -2\sqrt{2} \ \ 2\\ -\sqrt{2} \ \ -1 \end{vmatrix};\begin{vmatrix} 2 \ \ 0\\ -1 \ \ 0 \end{vmatrix} \right )=(0;4\sqrt{2};0)\)
\(\overrightarrow{SB}=(0;1;-2\sqrt{2}), \overrightarrow{SN}=(0;-\frac{1}{2};-\sqrt{2})\)
\(V_{SAMB}=\frac{1}{6}\left | \left [ \overrightarrow{SA}; \overrightarrow{SM}.\overrightarrow{SB} \right ] \right | = \frac{1}{6}\left | 0.0+4\sqrt{2}+0.(-2\sqrt{2}) \right |=\frac{2}{3}\sqrt{2}\)
\(V_{SAMN}=\frac{1}{6}\left | \left [ \overrightarrow{SA}; \overrightarrow{SM}.\overrightarrow{SN} \right ] \right | = \frac{1}{6}\left | 0.0+4\sqrt{2}.(-\frac{1}{2})+0.(-\sqrt{2}) \right |=\frac{\sqrt{2}}{3}\)
\(V_{SABMN}=V_{SAMB}+V_{SAMN}=\frac{2}{3}\sqrt{2}+\frac{1}{3}\sqrt{2}=\sqrt{2}\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



