Bài 6: Ứng dụng tính đơn điệu chứng minh bất đẳng thức

Bài giảng ứng dụng tính đơn điệu chứng minh bất đẳng thức  gồm có 2 phần nội dung chính:

• Lý thuyết
• Các ví dụ cụ thể nhằm giúp các em chứng minh được đồng biến và nghịch biến.

1. Lý thuyết 
 Hàm số y = f(x) đồng biến trên (a;b) nếu \(\left\{\begin{matrix} x_1,x_2\in (a;b)\\ x_1<x_2 \end{matrix}\right.\Rightarrow f(x_1)<f(x_2)\)
Hàm số y = f(x) nghịch biến trên (a;b) nếu \(\left\{\begin{matrix} x_1,x_2\in (a;b)\\ x_1<x_2 \end{matrix}\right.\Rightarrow f(x_1)>f(x_2)\)
2. Ví dụ 
VD1: Chứng minh \(sinx<x< tanx,\forall x\in (0;\frac{\pi}{2})\)
Giải
\(sin.sinx<x,\forall x\in (0;\frac{\pi}{2})\)
Xét \(f(x)=sinx-x\) trên \((0;\frac{\pi}{2})\)
\(f'(x)=cosx-1\leq 0\)
\(f(x)=0\Leftrightarrow x=0\) do \(x\in \left [ 0;\frac{\pi}{2} \right ]\)
f(x) nghịch biến trên \(\left [ 0;\frac{\pi}{2} \right ]\)
\(0<x<\frac{\pi}{2}\Rightarrow f(0)>f(x)\)
\(\Rightarrow 0>sinx-x\)
\(sinx<tanx,\forall x\in (0;\frac{\pi}{2})\)
Xét \(f(x)=tanx-x\) trên \((0;\frac{\pi}{2})\)
\(f'(x)=-\frac{1}{cos^2x}-1=\frac{1-cos^2x}{cos^2x}=\frac{sin^2x}{cos^2x}\geq 0\)
\(f'(x)=0\Leftrightarrow sinx=0\Leftrightarrow x=0\)
f(x) đồng biến trên \(\left [ 0;\frac{\pi}{2} \right )\) 
\(0<x<\frac{\pi}{2}\Rightarrow f(0)<f(x), (do \ x\in \left [ 0;\frac{\pi}{2} \right ])\)
\(\Rightarrow 0<tanx-x\)
\(\Rightarrow x<tanx\)
VD2: Chứng minh rằng  \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geq \frac{3}{2} \ \forall a,b,c>0\)
Giải
Không mất tính quát giả sử \(a\geq b\geq c>0\)
Đặt x = a, ta có \(x\geq b\geq c>0\)
Xét \(f(x)=\frac{x}{b+c}+\frac{b}{c+x}+\frac{c}{x+b}\) nên \([b;+\infty )\)
\(f'(x)=\frac{1}{b+c}-\frac{b}{(c+x)^2}-\frac{c}{(x+c)^2}\geq \frac{1}{b+c}-\frac{b}{(b+c)^2}-\frac{c}{(b+c)^2}=0\)
\(f'(x)=0\Leftrightarrow x=b=c\)
​f(x) đồng biến trên \([b;+\infty )\)

\(x\geq b\Rightarrow f(x)\geq f(b)=\frac{2b}{b+c}+\frac{c}{2b}\)
Đặt y = b, \(y\geq c\)
Xét \(g(y)=\frac{2y}{y+c}+\frac{c}{2y}\) trên \([c;+\infty )\)
\(g'(y)=\frac{2(y+c)-2y}{(y+c)^2}-\frac{c}{2y^2}\)
\(=\frac{2c}{(y+c)^2}-\frac{c}{2y^2}=C.\frac{4y^2-(y+c)^2}{2y^2(y-c)^2}\geq 0\)
\(g'(y)=0\Leftrightarrow y=c\)
g(y) là hàm số đồng biến trên \([c;+\infty )\)
\(y\geq c\Rightarrow g(y)\geq g(c)=\frac{2c}{2c}+\frac{c}{2c}=\frac{3}{2}\)
Vậy \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geq \frac{3}{2}\)
Dấu đẳng thức khi a=b=c
VD3: Cho x, y, z không âm x+y+z=1. CMR: \(xy+yz+xz-2xyz\leq \frac{7}{27}\). Không mất tính tổng quát giả sử.
Giải
\(x=min\left \{ x,y,z \right \}\)
\(3x\leq x+y+z\Rightarrow 3x\leq 1\Rightarrow x\leq \frac{1}{3}\)
\(A=xy+yz+xz-2xyz-\frac{7}{27}\)
\(=x(y+z)+yz(1-2x)-\frac{7}{27}\)
\(\leq x(1-x)+\frac{(y+2)^2}{2}(1-2x)-\frac{7}{27}\)

\(A\leq x(1-x)+\frac{(1-x)^2}{2}(1-2x)-\frac{7}{27}\)
\(A\leq x-x^2+\frac{1}{4}(1-2x+x^2)(1-2x)-\frac{7}{27}\)
\(\leq x-x^2+\frac{1}{2}x^3+\frac{5}{4}x^2-x+\frac{1}{4}-\frac{7}{27}\)
Xét \(f(x)=\frac{1}{2}x^3+\frac{1}{4}x^2-\frac{1}{108}\) nên \([0;\frac{1}{3})\)
\(f'(x)=-\frac{3}{2}x^2+\frac{1}{2}x=\frac{1}{2}x(-3x+1)\geq 0\)
\(f'(x)=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=0\\ x=\frac{1}{3} \end{matrix}\)
f(x) đồng biến trên \([0;\frac{1}{3}]\)
\(0\leq x\leq \frac{1}{3}\Rightarrow f(x)\leq f(\frac{1}{3})=0\)
\(A\leq f(x)\leq 0\)
hay \(xy+yz+xz-2xyz\leq \frac{7}{27}\)
Dấu đẳng thức xảy ra khi x = y = z= \(\frac{1}{3}\)
VD4: Cho x,y \(\geq 0,x+y=2. \ CMR \ x^2y^2(x^2+y^2)\leq 2\)

Giải
\(x^2+y^2=(x+y)^2-2xy=4-2xy\)
\(xy\leq \left ( \frac{x+y}{2} \right )=1\)
Vậy \(0\leq xy\leq 1\)
Đặt t=xy, ta có 
\(x^2y^2(x^2+y^2)=t^2(4-2t)\)
Xét \(f(t)=4t^2-2t^3\) trên [0;1]
\(f'(t)=8t-6t^2=t(8-6t)\geq 0\)
\(f(t)=0\Leftrightarrow \bigg \lbrack\begin{matrix} t=0\\ t=\frac{1}{3} \ (loai) \end{matrix}\)
(t) đồng biến trên [0;1]
\(0\leq t\leq 1\Rightarrow f(t)\leq f(1)=2\)
Vậy \(x^2y^2(x^2+y^2)\leq 2\)
Dấu đẳng thức khi x = y =1 
VD5: a) CMR: \(\frac{x+1}{\sqrt{x^2-x+1}}\leq 2 \ \ \forall x\in R\)
b) CMR:\(\sqrt{x^2-x+1}+\sqrt{y^2-y+1}+\sqrt{z^2-z+1}\geq 3\)
Với \(\forall x,y,z\) thỏa mãn \(x+y+z=3\)
Giải
a) Xét \(f(x)=\frac{x+1}{\sqrt{x^2-x+1}}\) trên R
\(f'(x)=\frac{\sqrt{x^2-x+1}-\frac{(2x-1)(2+1)}{2\sqrt{x^2-x+1}}}{x^2-x+1}-\frac{-3x+3}{2(x^2-x+1)\sqrt{x^2-x+1}}\)
\(f'(x)=0\Leftrightarrow x=1\)

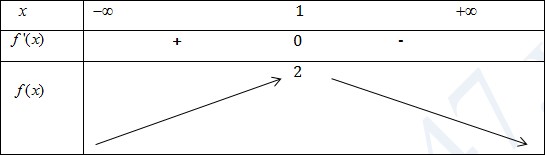
\(f(x)\leq 2\) (đpcm). Dấu đẳng thức xảy ra khi x= 1

b)
Từ (a) \(\frac{x+1}{\sqrt{x^2-x+1}}\leq 2\)
\(\Rightarrow \frac{1}{2}(x+1)\leq \sqrt{x^2-x+1}\)
Tương tự \(\Rightarrow \frac{1}{2}(y+1)\leq \sqrt{y^2-y+1}\)
\(\frac{1}{2}(z+1)\leq \sqrt{z^2-z+1}\)
\(\Rightarrow \frac{1}{2}(x+y+z+3)\leq \sqrt{x^2-x+1}+ \sqrt{y^2-y+1}+ \sqrt{z^2-z+1}=A\)
\(3\leq A\)(đpcm)

Dấu đẳng thức xảy ra khi x = y=  z =1