Bài 5: Tổng hợp dao động

Kiến thức các em có được sau khi hoàn thành bài Tổng hợp dao động là:

• Biểu diễn một dao động điều hòa bằng một vecto.
• Tổng hợp 2 dao động điều hòa cùng phương, cùng tần số.
• Nắm được một số phương pháp tổng hợp dao động
• Sử dụng máy tính bỏ túi, toán học để giải các bài toán về tổng hợp dao động.

Hôm nay chúng ta tiếp tục học bài 5: Tổng hợp dao động, đây là bài cuối cùng của chuyên đề 1.

Tổng hợp dao động là nói gọn, nói chính xác đó là tổng hợp hai dao động điều hòa cùng phương, cùng tần số.

Trước khi nói về tổng hợp dao động là gì? Chúng ta nhắc lại một số kiến thức.

* Biểu diện một dao động điều hòa bằng một vectơ
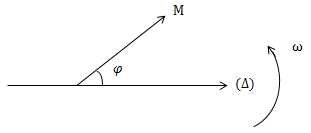
Xét dao động \(x = A\cos (\omega t + \varphi )\) được biểu diễn thành vectơ \(\overrightarrow{OM}\)
Với \(\overrightarrow{OM} \left\{\begin{matrix} |\overrightarrow{OM}| = A \ \ \ \ \\ (\overrightarrow{OM},\Delta ) = \varphi \end{matrix}\right.\)

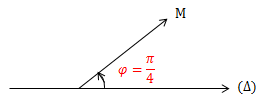
VD: \(x = 5 \cos (2 \pi t + \frac{\pi}{4}) \ (cm)\)

Xét 2 dao động: \(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \varphi _1)\\ x_2 = A_2 \cos (\omega t + \varphi _2) \end{matrix}\right.\)
* Độ lệch pha: \(\Delta \varphi = (\omega t + \varphi _2) - (\omega t + \varphi _1)\)
\(\Rightarrow \Delta \varphi = \varphi _2 - \varphi _1\)
• Nếu \(\Delta \varphi > 0 \Leftrightarrow \varphi _2 > \varphi _1\): x₂ sớm pha hơn x₁
• Nếu \(\Delta \varphi < 0 \Leftrightarrow \varphi _2 < \varphi _1\): x₂ trễ pha hơn x₁

* Tổng hợp 2 dao động điều hòa cùng phương, cùng tần số. (P² vectơ quay ≡ P² Frexnen)
Xét 2 dao động cùng phương, cùng tần số:
\(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \varphi _1)\\ x_2 = A_2 \cos (\omega t + \varphi _2) \end{matrix}\right.\)
Dao động tổng hợp \(x =x_1 + x_2 = A \cos (\omega t + \varphi )\)
\(\Rightarrow \overrightarrow{A} = \overrightarrow{A_1} + \overrightarrow{A_2}\ (*)\)

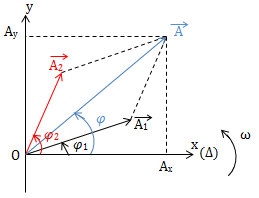
Chiếu (*) lên: \(\left\{\begin{matrix} Ox: A_x = A_{1x} + A_{2x} \\ Oy: A_y = A_{1y} + A_{2y} \end{matrix}\right.\)
Với \(A_x = A\cos \varphi ;\ Ay = A\sin \varphi\)
\(\Rightarrow \left\{\begin{matrix} A\cos \varphi = A_1 \cos \varphi _1 + A_2 \cos \varphi _2\\ A\sin \varphi = A_1 \sin \varphi _1 + A_2 \sin \varphi _2 \end{matrix}\right.\)
\(\Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2A_1A_2\cos (\varphi _2 - \varphi _1)}\)
\(\Rightarrow \tan \varphi = \frac{A_1 \sin \varphi _1 + A_2 \sin \varphi _2}{A_1 \cos \varphi _1 + A_2 \cos \varphi _2}\)

* Các trường hợp đặc biệt
\(+\ \Delta \varphi = \varphi _2 - \varphi _1 = k2 \pi\): x₁, x₂ cùng pha \(\Rightarrow \left\{\begin{matrix} A = A_1 + A_2\\ \varphi = \varphi _1 = \varphi _2 \end{matrix}\right.\)
\(+\ \Delta \varphi = \varphi _2 - \varphi _1 = (2k + 1) \pi\): x₁, x₂ ngược pha \(\Rightarrow \left\{\begin{matrix} A = |A_1 - A_2| \ \ \ \ \ \ \ \ \\ \varphi = \varphi _1 \ neu\ A_1 > A_2 \end{matrix}\right.\)
\(+\ \Delta \varphi = (2k + 1) \frac{\pi}{2} \Rightarrow x_1 \perp x_2 \Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2}}\)
NHỚ: \(|A_1 - A_2| \leq A \leq A_1 + A_2\)

VD1: Tổng hợp các dao động sau:
\(\\ a/ \left\{\begin{matrix} x_1 = 2 \cos (2 \pi t - \pi )\\ x_2 = 3 \cos (2 \pi t + \pi ) \end{matrix}\right. \\ b/ \left\{\begin{matrix} x_1 = 5 \cos ( \pi t - \frac{\pi }{3})\\ x_2 = \cos ( \pi t + \frac{2\pi }{3}) \end{matrix}\right. \\ c/ \left\{\begin{matrix} x_1 =6 \cos 4 \pi t \ \ \ \ \ \ \ \\ x_2 = 6 \cos (4 \pi t + \frac{\pi }{3}) \end{matrix}\right. \\ d/ \left\{\begin{matrix} x_1 = 4 \cos (5 \pi t + \frac{\pi }{6}) \ \ \ \ \\ x_2 = 4\sqrt{3} \cos (5 \pi t - \frac{\pi }{3}) \end{matrix}\right.\)
Giải:
a/ \(\Delta \varphi = \pi - (- \pi) = 2 \pi\): x₁, x₂ cùng pha
\(\Rightarrow \left\{\begin{matrix} A = A_1 + A_2 = 2 + 3 = 5 \ cm\\ \varphi = \pi ;\ \varphi =- \pi \hspace{2,3cm} \end{matrix}\right.\)

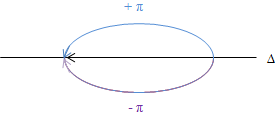
\(\rightarrow x = 5\cos (2 \pi t \pm \pi )\ (cm)\)
b/ \(\Delta \varphi = \frac{2 \pi}{3} - \frac{\pi }{3} = \pi\): x₁, x₂ ngược pha
\(\Rightarrow \left\{\begin{matrix} A = |A_1 - A_2| = |5-1| = 4 \ cm\\ \varphi = \varphi _1 = -\frac{\pi }{3}\ (Vi\ A_1 > A_2) \ \ \ \ \end{matrix}\right.\)
\(\rightarrow x = 4 \cos (\pi t - \frac{\pi}{3}) \ (cm)\)
c/ \(\left\{\begin{matrix} x_1 = 6 \cos 4 \pi t \ (cm) \ \ \ \ \ \ \ \rightarrow \left\{\begin{matrix} A_1 = 6 \ cm\\ \varphi _1 = 0 \ \ \ \ \end{matrix}\right.\\ x_2 = 6 \cos (4 \pi t + \frac{\pi}{3}) \ (cm) \rightarrow \left\{\begin{matrix} A_2 = 6\ cm\\ \varphi _2 = \frac{\pi }{3} \ \ \ \ \end{matrix}\right. \end{matrix}\right.\)
\(\cdot \ A = \sqrt{6^2 + 6^2 + 2.6.6 \cos \frac{\pi}{3}} = 6\sqrt{3}\ cm\)
\(\cdot \ \tan \varphi = \frac{6.\sin 0 + 6. \sin \frac{\pi }{3}}{6. \cos 0 + 6.\cos \frac{\pi }{3}} = \frac{3\sqrt{3}}{9} = \frac{\sqrt{3}}{3} \Rightarrow \varphi = \frac{\pi }{6}\)
d/ \(\left\{\begin{matrix} x_1 = 4\cos (4\pi t + \frac{\pi}{6})\ (cm)\ \ \ \ \\ x_2 = 4\sqrt{3} \cos (5 \pi t - \frac{\pi }{3})\ (cm) \end{matrix}\right.\)
\(\Delta \varphi = \frac{\pi }{2} - \left ( - \frac{\pi}{3} \right ) = \frac{\pi }{2}\)
\(A = \sqrt{A_{1}^{2} + A_{2}^{2}} = 8 \ (cm)\)
\(\tan \varphi = \frac{4 \sin \frac{\pi}{6} + 4\sqrt{3} \sin -\left ( - \frac{\pi}{3} \right )}{4 \cos \frac{\pi}{6} + 4\sqrt{3} \cos -\left ( - \frac{\pi}{3} \right )} = \frac{-4}{4\sqrt{3}}\)
\(\rightarrow \tan \varphi = -\frac{1}{\sqrt{3}} \Rightarrow \varphi = -\frac{\pi }{6}\)
\(\rightarrow x = 8\cos (5 \pi t - \frac{\pi }{6})\ (cm)\)
* Tổng hợp dao động điều hòa bằng máy tính
Cài đặt:
• Shift → mode → 4: R
• mode → 2: CMPLX
\(\left\{\begin{matrix} x_1 = A_1\cos (\omega t + \varphi _1) \rightarrow A_1 < \varphi _1 \hspace{3cm}\\ x_2 = A_2\cos (\omega t + \varphi _2) \rightarrow A_2 < \varphi _2 \ \ \ \ \ shift \rightarrow (-) \end{matrix}\right.\)
\(x = x_1 + x_2 = A\cos (\omega t + \varphi )\)
\(A_1 < \varphi _1 + A_2 < \varphi _2 \ \ \ \ \ Shift \rightarrow 2 \rightarrow 3 \ \ \ = A < \varphi\)

VD2: Cho 2 dao động cùng phương, cùng tần số có phương trình \(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \frac{\pi }{3})\ (cm)\\ x_2 = A_2 \cos (\omega t - \frac{\pi }{2})\ (cm) \end{matrix}\right.\)
Dao động tổng hợp \(x = x_1 + x_2 = 6\sqrt{3}\cos (\omega t + \varphi )\). Tìm giá trị lớn nhất của A₂ khi thay đổi A₁?
Giải:

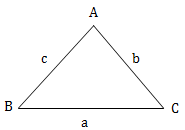
Định lý sin: \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\)

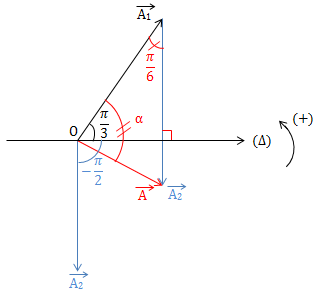
\(x=x_1 + x_2 \Rightarrow \overrightarrow{A} = \overrightarrow{A_1} + \overrightarrow{A_2}\)
Ta có: \(\frac{A_2}{\sin \alpha } = \frac{A}{\sin \frac{\pi }{6}} \Rightarrow A_2 = \frac{A}{\sin \frac{\pi }{6}}. \sin \alpha\)
\(\Rightarrow A_2 = \frac{6\sqrt{3}}{\frac{1}{2}}.\sin \alpha = 12\sqrt{3}.\sin \alpha\)
\(\Rightarrow (A_2)_{max} = 12 \sqrt{3}\ (cm) \Leftrightarrow \sin \alpha = 1 \Rightarrow \alpha = \frac{\pi }{2}\)