GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
1. Thể tích khối chóp
\(V=\frac{1}{3}S.h\)
S: diện tích đáy
h: chiều cao
2. Thể tích khối lăng trụ
V = S. h
S: diện tích đáy
h: chiều cao
Chú ý:
1) Hình chóp đều
+ Đáy là đa giác đều
+ Hình chóp đỉnh \(\equiv\) tâm đáy
Nhận xét:
+ Hình chóp đều có các cạnh bên bằng nhau.
+ Cạnh bên chưa chắc bằng cạnh đáy
2) Hình chóp tam giác đều (h/c đều)
\(\neq\) Hình chóp có đáy là tam giác đều.
3) Hình chóp tứ giác đều (h/c đều)
+ Đáy là hình vuông
+ H/c đỉnh \(\equiv\) tâm đáy
4) Lăng trụ đều
+ Lăng trụ đứng (cạnh bên vuông góc đáy)
+ Đáy là đa giác đều.
5) Lăng trụ tam giác đều (Lăng trụ đều)
\(\neq\) Lăng trụ có đáy là tam tác đều.
6) Lăng trụ tứ giác đều
+ Đáy là hình vuông
+ Lăng trụ đứng (Cạnh bên vuông góc đáy)
3. Phương pháp tính thể tích
1) \(\frac{V_1}{V_2}=\frac{h_1}{h_2}\) nếu 2 khối chóp (lăng trụ) có cùng diện tích đáy
2) Nếu 2 khối chóp (lăng trụ) có cùng chiều cao thì \(\frac{V_1}{V_2}=\frac{S_1}{S_2}\)
3) Bổ đề thể tích
\(\frac{V_{SA'B'C'}}{V_{SABC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}\)
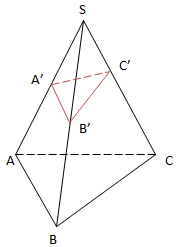
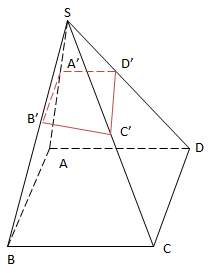
Chú ý: Đối với hình chiếu S.ABCD
\(\frac{V_{SA'B'C'D'}}{V_{SABCD}}\neq \frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC} .\frac{SD'}{SD}\)
Ví dụ 1: Phân chia khối hộp ABCD. A'B'C'D' thành 5 khối chóp tam giác
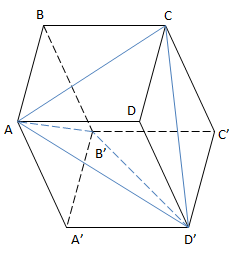
5 Khối chóp tam giác là:
A.A'B'D', C.B'C'D', B'.ABC, D'.ADC, A.CD'B'
+ Nếu thể tích khối hộp ABCD.A'B'C'D' là V
\(V_{A.A'B'D'}=V_{C.B'C'D'}=V_{B'ABC}=V_{D'ADC}=\frac{1}{6}V\)
\(V_{A.CD'B'}=\frac{1}{3}V\)
Câu 1: Cho khối hộp chữ nhật ABCD.A'B'C'D' AB = 2, AD = 3, AA' =4. Thể tích của khối chóp A.A'B'D' là?
Giải
\(V_{A.A'B'D'}=\frac{1}{6}V_{K. hop}=\frac{1}{6}.2.3.4=4\) (đvtt)
Câu 2: Cho khối hộp chữ nhật ABCD.A'B'C'D' AB = 2, AD = 3, AA' =4. Thể tích của khối chóp A.CB'D' là?
Giải
\(V_{A.CB'D'}=\frac{1}{3}V_{K. hop}=\frac{1}{3}.2.3.4=8\) (đvtt)
Câu 3: Cho khối hộp chữ nhật ABCD.A'B'C'D' biết VACB'D' =10(cm3). Tính Vkhối hộp.
Giải
\(V_{khoi \ hop}=3.V_{ACB'D'}=30(cm^3)\)
Câu 4: Cho khối tứ diện gần đều ABCD, AB = CD = a, AD = BC = b, AC = BD = c. Tính VABCD
Giải
\(\left\{\begin{matrix} x^2+y^2=c^2\ \ (1)\\ x^2+z^2=b^2\ \ (2)\\ y^2+z^2=a^2 \ \ (3) \end{matrix}\right.\)
\(\Rightarrow x^2+y^2+z^2=\frac{1}{2}(a^2+b^2+x^2)(4)\)
Trừ vế theo vế (4) cho (1) (2) (3) ta có
\(\begin{matrix} x^2=\frac{1}{2}(-a+b^2+c^2)\\ \\ y^2=\frac{1}{2}(a^2-b^2+c^2)\\ \\ z^2=\frac{1}{2}(a^2+b^2-c^2) \end{matrix}\)\(V_{hop}=xyz=\frac{1}{2\sqrt{2}}.\sqrt{(-a^2+b^2+c^2)(a^2-b^2+c^2)(a^2+b^2-c^2)}\)
\(V_{ABCD}=\frac{1}{3}V_{hop}=\frac{1}{6\sqrt{2}}.\sqrt{ (-a^2+b^2+c^2)(a^2-b^2+c^2)(a^2+b^2-c^2)}\)
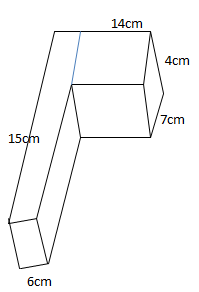
Ví dụ 2: Tính thể tích của khối sau:
\(V=V_{Kh1}+V_{Kh2}\)
\(=4.6.15+14.4.7=360+392=752(cm^3)\)
Ví dụ 3: Tính thể tích của khối đa diện sau.
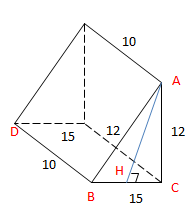
\(V=\frac{1}{3}S.h=\frac{1}{3}.\frac{1}{2}.AH.BC.BD\)
\(=\frac{1}{6}.\sqrt{12^2-(\frac{15}{2})^2}.15.10=\frac{1}{6}.\sqrt{24^2-15^2}.15.5\)
\(=\frac{75}{6}.\sqrt{9.39}=\frac{75}{2}\sqrt{39}\) (đvtt)
Ví dụ 4: Tính thể tích của sau:
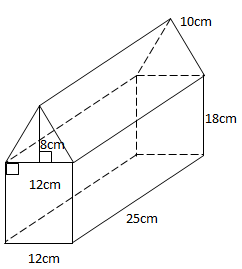
\(V=V_{lang \ tru}+ V_{hop}=\frac{18}{2}.12.25+12.25.18\)
\(=12.25 .(4+18)=300.22=6600(m^3)\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



