Bài 15: Bài toán về vị trí tương đối giữa các đường thẳng

I. Lý thuyết
\(\Delta _1\) đi qua M₁ và có 1 VTCP \(\overrightarrow{u_1}\)
\(\Delta _2\) đi qua M₂ và có 1 VTCP \(\overrightarrow{u_2}\)

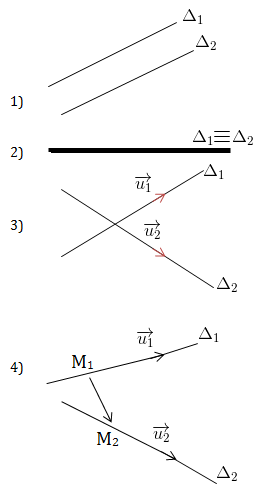
1) \(\Delta _1\), \(\Delta _2\) chéo nhau
\(\Leftrightarrow \left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]. \overrightarrow{M_1.M_2}\neq 0\)
2)
\(\Delta _1\), \(\Delta _2\) cắt nhau
\(\Leftrightarrow \left\{\begin{matrix} \left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]. \overrightarrow{M_1.M_2}= 0\\ \overrightarrow{u_1}\neq k. \overrightarrow{u_2} \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix}\right.\)
3)
\(\Delta _1\) // \(\Delta _2\)
\(\Leftrightarrow \left\{\begin{matrix} \overrightarrow{u_1}=k.\overrightarrow{u_2}\\ M_1\in \Delta _1, M_1\notin \Delta _2 \end{matrix}\right.\)
4)
\(\Delta _1\equiv \Delta _2 \Leftrightarrow \left\{\begin{matrix} \overrightarrow{u_1}=k.\overrightarrow{u_2}\\ M_1\in \Delta _1, M_1\in \Delta _2 \end{matrix}\right.\)
II. Bài tập
VD1: Xét vị trí tương đối của các đường thẳng sau đây \(\Delta _1:\frac{x-1}{2}=\frac{y}{3}=\frac{z+2}{-1}; \ \Delta _2:\left\{\begin{matrix} x=t\\ y=2t\\ z=1+2t \end{matrix}\right.\)
Giải
\(\Delta _1\) đi qua M₁(1;0;-2), có 1 VTCP \(\overrightarrow{u_1}=(2;3;-1)\)
\(\Delta _2\) đi qua M₂(1;0;-2), có 1 VTCP \(\overrightarrow{u_2}=(1;2;2)\)
\(\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]= \left ( \begin{vmatrix} 3 \ \ -1\\ 2 \ \ \ \ 2 \end{vmatrix}; \begin{vmatrix} -1 \ \ 2\\ 2 \ \ 1 \end{vmatrix};\begin{vmatrix} 2 \ \ 3\\ 1 \ \ \ 2 \end{vmatrix} \right )=(8;-5;1)\)
\(\overrightarrow{M_1M_2}=(-1;0;3)\)
\(\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ].\overrightarrow{M_1M_2}= 8.(-1)+(-5).0+1.3=-5\neq 0\)
Vậy \(\Delta _1\), \(\Delta _2\) chéo nhau.
VD2: Xét vị trí tương đối giữa các đường thẳng
\(\Delta _1:\left\{\begin{matrix} x=1+t\\ y=2-t\\ z=3+2t \end{matrix}\right. \ \ \Delta _2:\left\{\begin{matrix} x=2t\\ y=3-2t\\ z=1+4t \end{matrix}\right.\)
Giải
\(\Delta _1\) đi qua M₁(1;2;3), có 1 VTCP \(\overrightarrow{u_1}=(1;-1;2)\)
\(\Delta _2\) đi qua M₂(0;3;1), có 1 VTCP \(\overrightarrow{u_2}=(2;-2;4)\)
\(\overrightarrow{u_2}=2\overrightarrow{u_1}\)
\(M_1\in \Delta _2\Leftrightarrow \left\{\begin{matrix} 1=2t\\ 2=3-2t\\ 3=1+4t \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} t=\frac{1}{2}\\ \\ t=\frac{1}{2}\\ \\ t=\frac{1}{2} \end{matrix}\right.\)
Vậy \(M_1\in \Delta _2\)
Vậy \(\Delta _1\equiv \Delta _2\)
VD3: Viết phương trình đường thẳng \(\Delta\) đi qua M(1;2;3) và song song với \(d:\left\{\begin{matrix} x=1-2t\\ y=2+t\\ z=-1-2t \end{matrix}\right.\)
Giải
\(\Delta\) // d nên \(\Delta\) nhận \(\overrightarrow{u_d}=(-2;1;-2)\) làm 1 VTCP
\(pt \ \Delta \left\{\begin{matrix} x=1-2t\\ y=2+t\\ z=3-2t \end{matrix}\right.\) (thỏa mãn vì \(M\in d\))
 

VD4: Cho \(d_1:\frac{x}{2}=\frac{y-1}{-1}=\frac{z+2}{1}\)
\(d_2:\left\{\begin{matrix} x=-1+2t\\ y=1+t\\ z=3 \end{matrix}\right.\)
a) CMR: d₁, d₂ chéo nhau
b) Viết phương trình đường thẳng \(\Delta \perp (P) \ \ 7x+y-4z=0\) đồng thời cắt hai đường thẳng d₁, d₂ 
Giải
a)
d₁ đi qua M₁(0;1;-2), có 1 VTVP \(\overrightarrow{u_1}=(2;-1;1)\)
d₂ đi qua M₂(-1;1;3), có 1 VTVP \(\overrightarrow{u_2}=(2;1;0)\)
\(\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]= \left ( \begin{vmatrix} -1 \ \1\\ 1 \ \ 0 \end{vmatrix};\begin{vmatrix} 1 \ \ 2\\ 0 \ \ 2 \end{vmatrix};\begin{vmatrix} 2 \ \ -1\\ 2 \ \ 1 \end{vmatrix} \right )=(-1;2;4)\)
\(\overrightarrow{M_1M_2}=(-1;0;5)\)
\(\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ].\overrightarrow{M_1M_2}= (-1).(-1)+2.0+4.5=21\neq 0\)
Vậy d₁,d₂ chéo nhau.
b)
Phân tích

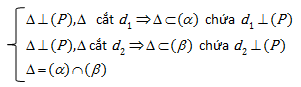
* Viết phương trình \((\alpha )\) chứa \(d_1, \perp (P)\)

\(\overrightarrow{n_\alpha }\perp \overrightarrow{u_1 }=(2;-1;1)\)
\(\overrightarrow{n_\alpha }\perp \overrightarrow{n_P}=(7;1;-4)\)
Chọn \(\overrightarrow{n_\alpha }=\left [ \overrightarrow{n_1 }; \overrightarrow{n_P }\right ]= \left ( \begin{vmatrix} -1 \ \ 1\\ 1 \ \ -4 \end{vmatrix}; \begin{vmatrix} 1 \ \ 2\\ -4 \ \ 7 \end{vmatrix}; \begin{vmatrix} 2 \ \ -1\\ 7 \ \ 1 \end{vmatrix} \right )=(3;15;9)\)
\(\Rightarrow \overrightarrow{n_\alpha }'=(1;5;3)\) là 1 VTPT \((\alpha )\)
\(M_1(0;1;-2)\in d_1\Rightarrow M_1(0;1;-2)\in (\alpha )\)
\(pt \ (\alpha ): 1(x-0)+5(y-1)+3(z+2)=0\)
\(\Leftrightarrow x+5y+3z+1=0\)
* Viết phương trình \((\beta )\) chứa d₂ và vuông góc (P)
\(\begin{matrix} \overrightarrow{n_\beta }\perp \overrightarrow{u_2 }=(2;1;0) \ \ \\ \overrightarrow{n_\beta }\perp \overrightarrow{n_P}=(7;1;-4) \end{matrix}\)
Chọn 
\(\overrightarrow{n_\beta }=\left [ \overrightarrow{u_2}; \overrightarrow{n_P} \right ]= \left ( \begin{vmatrix} 1\ \ 0\\ 1 \ \-4 \end{vmatrix};\begin{vmatrix} 0\ \ 2\\ -4 \ \7 \end{vmatrix}\begin{vmatrix} 2\ \ 1\\ 7 \ \1 \end{vmatrix} \right )=(-4;8;-5)\)
\(M_2(-1;1;3)\in d_2\Rightarrow M_2\in (\beta )\)
\(pt (\beta ): -4(x+1)+8(y-1)-5(z-3)=0\)
\(\Leftrightarrow -4x+8y-5z+3=0\)
\(\Delta =(\alpha )\cap (\beta )\)
Cho y = 0 ta có \(\left\{\begin{matrix} x+3z+1=0\\ -4x-5z+3=0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=2\\ z=-1 \end{matrix}\right.\)
\(M(2;0;-1)\in \Delta\)
\(\overrightarrow{u}\perp \overrightarrow{n_\alpha }'=(1;5;3)\)
\(\overrightarrow{u}\perp \overrightarrow{n_\beta }'=(-4;8;-5)\)
Chọn
\(\overrightarrow{u}=\left [ \overrightarrow{n_\alpha }';\overrightarrow{n_\beta} \right ]=\left ( \begin{vmatrix} 5 \ \ 3\\ 8 \ \ -5 \end{vmatrix}; \begin{vmatrix} 3 \ \ 1\\ -5 \ \ -4 \end{vmatrix};\begin{vmatrix} 1 \ \ 5\\ -4 \ \ 8 \end{vmatrix}\right )=(-49;-7;28)\)
hay \(\overrightarrow{u}'=(-7;-1;4)\) là 1 VTCP \(\Delta\)
\(pt \ \Delta \left\{\begin{matrix} x=2-7t\\ y=0-t\\ z=-1+4t \end{matrix}\right.\)
Cách 2:
\(A=\Delta \cap d_1\Rightarrow A\in d_1\Rightarrow A(2a;1-a;2+a)\)
\(B=\Delta \cap d_2\Rightarrow B\in d_2\Rightarrow B(-1+2t;1+t;3)\)
\(\overrightarrow{AB}=(-1+2t-2a;t+a;1-a)\)
\(A,B\in \Delta , \ \ \Delta \perp (P)\Rightarrow \overrightarrow{AB}=k.\overrightarrow{n_P}\)
\(\left\{\begin{matrix} -1+2t-2a=7k\\ t+a=k\\ 1-a=-4k \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} a=1+4k \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ t+1+4k=k \ \ \ \ \ \ \ \ \ \ \ \ \ \\ -1+2t-2-8k=7k\ \ \ \ \end{matrix}\right.\Rightarrow \left\{\begin{matrix} t-3k=-1\\ 2t-15k=3\\ a=1+4k \end{matrix}\right.\Rightarrow \left\{\begin{matrix} k=-\frac{5}{9}\\ \\ t=-\frac{8}{3}\\ \\ a=-\frac{11}{9} \end{matrix}\right.\)
\(\Rightarrow \overrightarrow{AB}=\left ( -\frac{35}{9};-\frac{5}{9};\frac{20}{9} \right )\)
\(A\left ( -\frac{22}{9};-\frac{2}{9};\frac{7}{9} \right )\)
\(Pt \ \Delta \left\{\begin{matrix} x=-\frac{22}{9}+7t\\ y=-\frac{2}{9}+t \ \ \ \ \\ z=\frac{7}{9}-4t \end{matrix}\right.\)