GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
\((\alpha _1) \ A_1x+B_1y+C_1z+D_1=0\)
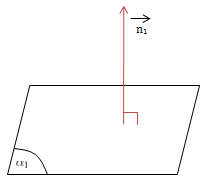
có 1 VTPT \(\vec{n_1}=(A_1;B_1;C_1)\)
\((\alpha _2) \ A_2x+B_2y+C_2z+D_2=0\)
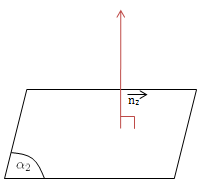
có 1 VTPT \(\vec{n_2}=(A_2;B_2;C_2)\)
1)
\((\alpha _1)//(\alpha _2)\)
\(\left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1\neq D_2 \end{matrix}\right.\)
Chú ý:
Nếu \(A_2, B_2, C_2, D_2 \neq 0\)
\((\alpha _1)//(\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}\neq \frac{D_1}{D_2}\)
2)
\((\alpha _1)\equiv (\alpha _2)\)
\(\Leftrightarrow \left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1=k. D_2 \end{matrix}\right.\)
Chú ý:
Nếu \(A_2, B_2, C_2, D_2 \neq 0\) thì
\((\alpha _1)\equiv (\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}= \frac{D_1}{D_2}\)
3)
\((\alpha _1),(\alpha _2)\) cắt nhau
\(\Leftrightarrow \vec{n_1}\neq k.\vec{n_2}\)
Chú ý:
Nếu \(A_2,B_2,C_2\neq 0\) thì
\((\alpha _1),(\alpha _2)\) cắt nhau \(\Leftrightarrow \Bigg \lbrack\begin{matrix} \frac{A_1}{A_2} \neq \frac{B_1}{B_2}\\ \frac{A_1}{A_2} \neq \frac{C_1}{C_2}\\ \frac{B_1}{B_2} \neq \frac{C_1}{C_2} \end{matrix}\)
II. Bài tập
VD1: Xét vị trí tương đối của các cặp mặt phẳng trong các trường hợp sau.
a) \(\begin{matrix} (P) \ \ x-2y+2z+1=0\\ (Q) \ \ 2x-4y+4z+3=0 \end{matrix}\)
b) \(\begin{matrix} (P) \ \ 2x-3y+4z-1=0\\ (Q) \ \ x+y-2z+3=0 \ \ \ \end{matrix}\)
c) \(\begin{matrix} (P) \ \ 3x-y-2z+1=0\\ (Q) \ \ 6x-2y-4z+2=0 \ \ \ \end{matrix}\)
Giải
a)
(P) có 1 VTPT \(\overrightarrow{n}_P=(1;-2;2)\)
(Q) có 1 VTPT \(\overrightarrow{n}_Q=(1;-4;4)\)
Ta có \(\frac{1}{2}=\frac{-2}{-4}=\frac{2}{4}\neq \frac{1}{3}\Rightarrow (P)//(Q)\)
b)
(P) có 1 VTPT \(\overrightarrow{n}_P=(2;-3;4)\)
(Q) có 1 VTPT \(\overrightarrow{n}_Q=(1;1;-2)\)
\(\frac{2}{1}\neq \frac{-3}{1}\)
Vậy (P), (Q) cắt nhau
c)
(P) có 1 VTPT \(\overrightarrow{n}_P=(3;-1;-2)\)
(Q) có 1 VTPT \(\overrightarrow{n}_Q=(6;-2;-4)\)
Ta có
\(\frac{3}{6}=\frac{-1}{-2}=\frac{-2}{-4}=\frac{1}{2}\)
Vậy \((P)\equiv (Q)\)
VD2: Cho \((P) \ (m+1)x+2y+z-1=0 \ , (Q) \ 3x+2y+(m-1)z-1=0\). Tìm m để
a) (P) // (Q)
b) (P) \(\equiv\) (Q)
c) (P), (Q) cắt nhau
Giải
a)
(P) có 1 VTPT \(\overrightarrow{n_P}=(m+1;2;1)\)
(Q) có 1 VTPT \(\overrightarrow{n_Q}=(3;2;m-1)\)
TH1:
m - 1 = 0 ⇔ m =1
\(\overrightarrow{n_P}=(2;2;1), \overrightarrow{n_Q}=(3;2;0)\)
\(\overrightarrow{n_P}\neq k.\overrightarrow{n_Q} \ \forall\) suy ra (P), (Q) cắt nhau
TH2:
m - 1 \(\neq 0\)
\((P) //(Q)\Leftrightarrow \frac{m+1}{3}=\frac{2}{2}=\frac{1}{m-1}\neq \frac{-1}{-1}\)
TH không xảy ra
Vậy không \(\exists m\) để (P) // (Q)
b)
\((P) \equiv (Q)\Leftrightarrow \frac{m+1}{3}=\frac{2}{2}=\frac{1}{m-1}=\frac{-1}{-1}\)
⇔ m = 2
Vậy \((P) \equiv (Q)\) khi m = 2
c)
(P), (Q) cắt nhau khi \(m\neq 2\)
VD3: Viết phương trình mặt phẳng (P) đi qua giao tuyến của \((Q) \ 3x -y+z-2=0 \ (R) \ x+4y-5=0\) và song song với \((\alpha ) \ 2x -z+7=0\)
Giải
(P) đi qua giao tuyến của (Q) và (R) nên có phương trình dạng
\(m(3x-y+z-2)+n(x+4y-5)=0 \ \ (m^2+n^2\neq 0)\)
\(\Leftrightarrow (3m+n)x+(-m+4x)y+mz-2m-5n=0\)
(P) có 1 VTPT \(\overrightarrow{n}_P=(3m+n;-m+4n;m)\)
\((\alpha )\) có 1 VTPT \(\overrightarrow{n}_\alpha =(2;0;-1)\)
\((P)//(\alpha )\) khi \(\left\{\begin{matrix} \vec{n}_P=k.\vec{n}_\alpha \ (1) \\ -2m-5n\neq 7k \ \ (2) \end{matrix}\right.\)
\((1)\Leftrightarrow \left\{\begin{matrix} 3m+n=2k\\ -m+4n=0\\ m=-1 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} m=-1\\ n=-\frac{1}{4}\\ k=-\frac{13}{8} \end{matrix}\right. \ (t/m \ (2))\)
Vậy (P): \(-\frac{13}{4}x-z+\frac{13}{4}=0\)
hay \(-13x-4z+13=0\)
VD4: Viết phương trình (P) đi qua giao tuyến của \((Q) \ 3x-y+z-2=0, \ (R) \ x +4y-5=0\) và vuông góc cới 2x - z + 7 = 0 \((\alpha )\)
Giải
(P) đi qua giao tuyến (Q) và (R) có phương trình dạng
\(m(3x-y+z-2)+n(x+4y-5)=0 \ \ (m^2+n^2\neq 0)\)
hay \((3m+n)x+(-m+4n)y+mz-2m-5n=0\)
(P) có 1 VTPT \(\vec{n}_P=(3m+n;-m+4n;m)\)
\((P)\perp (\alpha )\Leftrightarrow \vec{n}_P.\vec{n}_\alpha =0\)
\(\Leftrightarrow 2(3m+n)+0(-m+4n)-m=0\)
\(\Leftrightarrow 5m+2n=0\)
\(\Leftrightarrow 5m=-2n\)
Chọn m = 2, n = -5
PT (P): x - 22y + 2z + 21 = 0














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



